[BZOJ4005][JLOI2015]骗我呢-[dp+容斥]

Description

传送门

Solution

如果单独考虑一行i，则左边位置的数严格比右边位置的数小。而一行有m个位置，它们可以填[0,m]这m+1个数，则必然有一个数不存在。

定义第i行的第j位突变需要满足$x[i][j+1]-x[i][j]>1$，此时不存在的数为j。

通过分析可以得到，假如在i-1行的突变位置为j+1，则第i行突变位置的合法范围为[j,m]。*

设f[i][j]为在第i行，突变位置为j的情况数。

则递推式为：$f[i][j]=f[i-1][j+1]+f[i][j-1]$。

因为当第i-1行在第j+1位突变，第i行的突变位置即为j。f[i][j-1]为在[0,j-1]位突变的情况数，由*可得知这些情况也同样可以在第j位突变。

特殊的，$f[i][0]=f[i-1][0]+f[i-1][1]$，$f[i][m]=f[i][m-1]$。

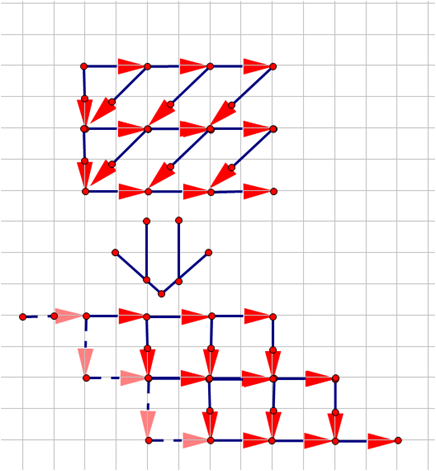
如图，我们把转移画出来后将第i行往右移i-1格并建立虚拟节点来满足f[i][0]的转移。

图中的n=3，m=3。

此时的点(n,n+m+1)[即为第n行第n+m个点]表示的并不是所有情况之和，而是第n行突变位置为m的情况数。

我们考虑多加一行一列，根据递推式，点(n+1,n+m+2)即为第n行所有情况之和了。

最后将得到图形补全为矩形后是会有n+1行n+m+2列。

将该图画在平面直角坐标系里（即将其翻转），则终点坐标为(n,n+m+1)

如图，直线y_a=x+1和直线y_b=x-(m+2)即为边界。

我们把多次越过同一边界视为只越过一次。则越界方案为ababa...或babab...。

则ans=总方案数-第一次越过a的次数-第一次越过b的次数。

对于先越过a的，考虑：-越界方案末尾为a的情况数+越界方案末尾为ba的方案数-越界方案末尾为aba的方案数。。。直到方案数为0。

对于越界方案末尾为a的情况数，为将整个图针对直线a翻转后(1,1)到对称终点的方案；当越界方案末尾为ba，则在上一个图的基础上把图沿着直线b翻转，计算(1,1)到本次到对称终点的方案数。

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
const int mod=1e9+;
int n,m;
ll fac[],inv[];
void pre()
{
    fac[]=inv[]=;
    fac[]=inv[]=;
    for (int i=;i<=;i++)
    {
        fac[i]=fac[i-]*i%mod;
        inv[i]=(mod-mod/i)*inv[mod%i]%mod;
    }
    for (int i=;i<=;i++) inv[i]=inv[i]*inv[i-]%mod;
}
ll C(int x,int y)
{
    if (x<y||x<||y<) return ;
    return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
ll cal(int x,int y)
{
    if (x<||y<) return ;return C(x+y,y);
}
void turnA(int &x,int &y)
{
    swap(x,y);
    x--;y++;
}
void turnB(int &x,int &y)
{
    swap(x,y);x+=m+;y-=m+;
}
ll ans;
int main()
{
    scanf("%d%d",&n,&m);
    pre();
    ans=cal(n+m+,n);
    int x=n+m+,y=n;
    while (x>=&&y>=)
    {
        turnA(x,y);ans=(ans-cal(x,y))%mod;
        turnB(x,y);ans=(ans+cal(x,y))%mod;
    }
    x=n+m+,y=n;
    while (x>=&&y>=)
    {
        turnB(x,y);ans=(ans-cal(x,y))%mod;
        turnA(x,y);ans=(ans+cal(x,y))%mod;
    }
    if (ans<) ans+=mod;
    cout<<ans;
}