hdu4255筛素数+广搜

Mr. B has recently discovered the grid named "spiral grid".
Construct the grid like the following figure. (The grid is actually infinite. The figure is only a small part of it.)

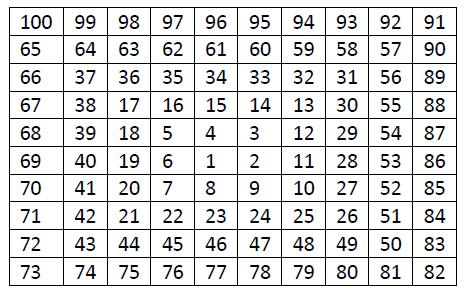
Considering
traveling in it, you are free to any cell containing a composite number
or 1, but traveling to any cell containing a prime number is
disallowed. You can travel up, down, left or right, but not diagonally.
Write a program to find the length of the shortest path between pairs of
nonprime numbers, or report it's impossible.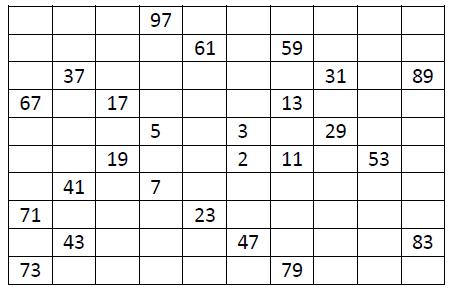

 

Input

Each test case is described by a line of input containing two nonprime integer 1 <=x, y<=10,000.

 

Output

For
each test case, display its case number followed by the length of the
shortest path or "impossible" (without quotes) in one line.

 

Sample Input

1 4
9 32
10 12

 

Sample Output

Case 1: 1
Case 2: 7
Case 3: impossible

 

 

 

 

 

 

 

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;
int book[401][401];
int a[401][401];
int b[401][401];
int vis[160005];
int prime[160005];
struct node
{
    int x;
    int y;
    int s;
} que[160005];
void make1()
{
   for(int i=1;i<=160001;i++)
   prime[i]=1;
        prime[1] = 0;
    for(int i = 2; i <= 160001; i++)
    {
        if(prime[i])
        {
            for(int j = 2*i; j <= 160001; j+=i)
                prime[j] = 0;
        }
    }

int x,y;
    int n=400;
    int tot=160000;
    a[0][0]=160000;
    x=0,y=0;
    while(tot>1)
    {
        while(y+1<n&&!a[x][y+1])
        {
            a[x][++y]=--tot;
        }
        while(x+1<n&&!a[x+1][y])
        {
            a[++x][y]=--tot;
        }

while(y-1>=0&&!a[x][y-1])
        {
            a[x][--y]=--tot;
        }
        while(x-1>=0&&!a[x-1][y])
        {
            a[--x][y]=--tot;
        }
    }
    for(int i=0; i<400; i++)

for(int j=0; j<400; j++)
        {
            if(prime[a[i][j]]==1)
                b[i][j]=1;
            else
                b[i][j]=0;
        }
}
int main()
{
    int t1,t2;
    int ans=0;
  make1();
    while(scanf("%d%d",&t1,&t2)!=EOF)
    {

int next[4][2]= {0,1,1,0,0,-1,-1,0};
        memset(book,0,sizeof(book));
        if(t1==t2)
            printf("Case %d: 0\n",++ans);
        else
        {
            int startx,starty,endx,endy;
            for(int i=0; i<=399; i++)
                for(int j=0; j<=399; j++)
                {
                    if(a[i][j]==t1)
                    {
                        startx=i;
                        starty=j;
                    }
                    if(a[i][j]==t2)
                    {
                        endx=i;
                        endy=j;
                    }
                }
            int head=1,tail=1;
            que[head].x=startx;
            que[head].y=starty;
            tail++;
            book[startx][starty]=1;
            int flag=0;
            while(head<tail)
            {
                for(int k=0; k<4; k++)
                {
                    int tx=que[head].x+next[k][0];
                    int ty=que[head].y+next[k][1];
                    if(tx<0||tx>399||ty<0||ty>399)
                        continue;
                    if(b[tx][ty]==0&&book[tx][ty]==0)
                    {
                        book[tx][ty]=1;
                        que[tail].x=tx;
                        que[tail].y=ty;
                        que[tail].s=que[head].s+1;
                        tail++;
                    }
                    if(tx==endx&&ty==endy)
                    {
                        flag=1;
                        break;
                    }
                }
                if(flag==1)
                    break;
                head++;
            }
            if(flag==1)
                printf("Case %d: %d\n",++ans,que[tail-1].s);
            else
                printf("Case %d: impossible\n",++ans);
        }
    }
    return 0;

}