python二叉树及叶节点获取 (面试题)

才疏学浅，智商不够，花了一晚上看了二叉树。记录一下：

1.二叉树的遍历

前序遍历：根节点->左子树->右子树

中序遍历：左子树->根节点->右子树

后序遍历：左子树->右子树->根节点

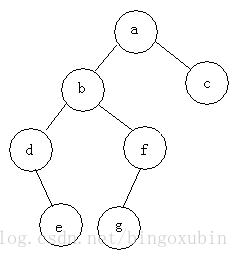
三层二叉树：
             A
         ↙  ↘
      B          C
   ↙ ↘     ↙ ↘
 D       E  F      G
前序：先把BDE,CFG看做是A的左右子节点，因此是从A开始读，A作为第一个，然后进到左子节点 BDE, 这时再把它看做一个小二叉树看待，其
顺序为BDF,读完这个，以A为根的三个结构就读完了根左，然后剩下CFG，这时在读CFG。到此为止，这组二叉树的前序组合为ABDRCFG,这种读法
从上往下，从根开始，把下面所有节点结构都以根左右的形式读取，遇到有子节点的情况变读左子节点，读完再读右。总结其格式：从根开始，找左，
以左为根，找左，若无，找右，以右为根，找左，若无，找右，若无，找上一级右，以此类推。

中序：先把BDE,CFG看做是A的左右子节点，A1，A2。中序的读法为左根右，A1，A，A2。然后再看A1，D为左，B为中，E为右，D为叶节点
（无子节点了），因此从D开始DBE，A1读完，然后为A，再看A2，A2为FCG，因此中序的顺序为：DBE>A>FCG。

后序：左右根，A1，A2，A。A1在左右根：DEB，A2是FGC，A1，A2，A便是DEBFGCA。

巩固练习：

前序遍历：abdefgc

中序遍历：debgfac

后序遍历：edgfbca

Q：寻找二叉树所有叶节点：

class Node(object):
    """节点类"""
    def __init__(self, val=-1, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Tree(object):
    """树类"""
    def __init__(self):
        self.root = Node()
        self.queue = []  #使用列表模拟队列

    def add(self, val):
        """为树添加节点"""
        node = Node(val)

        if self.root.val == -1:  # 如果树是空的，则对根节点赋值

            self.root = node
            self.queue.append(self.root)
        else:
            treeNode = self.queue[0]  # 此结点的子树还没有齐。
            if treeNode.left == None:
                treeNode.left = node　　# 左子树变成节点（初始此节点左右都是None）
                self.queue.append(treeNode.left)
            else:
                treeNode.right = node
                self.queue.append(treeNode.right)
                self.queue.pop(0)  # 如果该结点存在右子树，将此结点丢弃。

    def leave(self,root):
        if root==None:
            return 0
        elif root.left ==None and root.right == None :
            return 1
        else:
            return (self.leave(root.left)+self.leave(root.right))   # 递归遍历所有左子树右子树，当左右都为None时才算1

if __name__ == '__main__':
    """主函数"""
    vals = range(10)           #生成十个数据作为树节点
    tree = Tree()          #新建一个树对象
    for val in vals:
        tree.add(val)           #逐个添加树的节点
    print ('叶子节点个数:', tree.leave(tree.root))

感谢：

https://blog.csdn.net/harrytsz/article/details/80866150

https://blog.csdn.net/qq_36197940/article/details/77482493

https://www.cnblogs.com/joangaga/p/7066551.html