利用xampp集成环境搭建pikachu靶场及部分问题解决

xampp的环境部署

1.本地服务器的搭建

首先要到官网下载xampp https://www.apachefriends.org/zh_cn/index.html

有各个不同的系统版本，这里我们选择windows系统的版本进行下载

下载完成完成后就是安装了，一直点击下一步选择好自己所要放置xampp的文件夹即可。

安装完毕后，打开xampp就来到软件页面如下

这我们搭建pikachu靶场需要开启Apache和MySQL，点击对应start就可以开启，而在开启Apache和MySQL时遇到无法正常开启而报错的情况可以查看日志找到错误寻找相应的解决方案。

我在开启Apache和MySQL时遇到的报错是Apache的端口冲突，所以这里我讲一下如何解决端口冲突问题

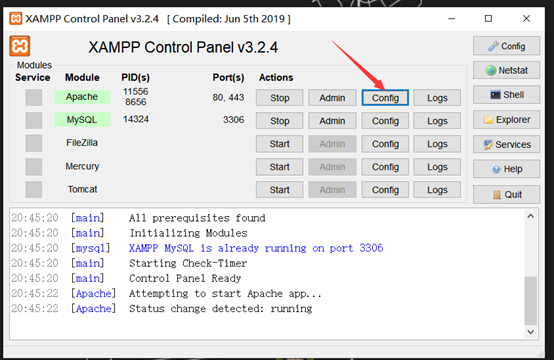
1.首先点击击Conflg

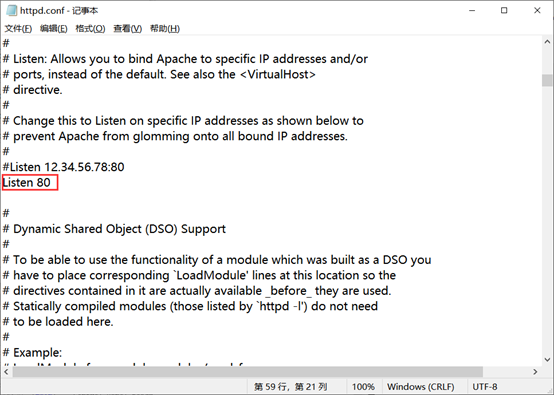
修改httpd.conf和httpd-ssl.conf两个文件的端口，将80和443修改成801和4431这样的没有被占用的端口

ps：不仅仅只是这两个地方的，文件里所有的80和443都要改成801和4431！！！

、

修改完毕后，保存关闭，打开Conflg，点击Service and settings。

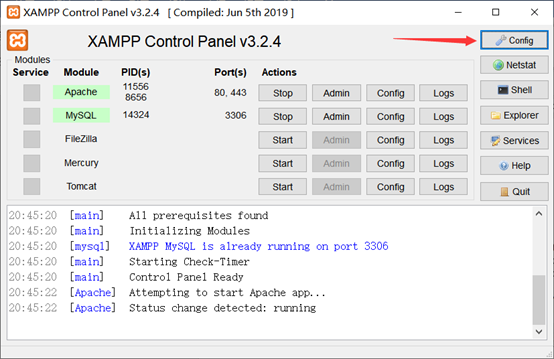
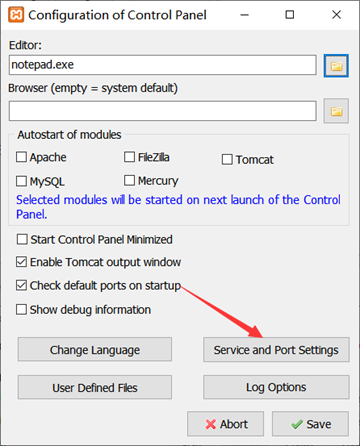
将80和433端口，改成自定义的端口如801,4331，点击save保存即可

如果点save保存时，遇到拒绝访问，原因是没有权限

要xampp文件夹中找到xampp-control文件给予管理员权限，先打开文件属性，点到安全页面，点击编辑。

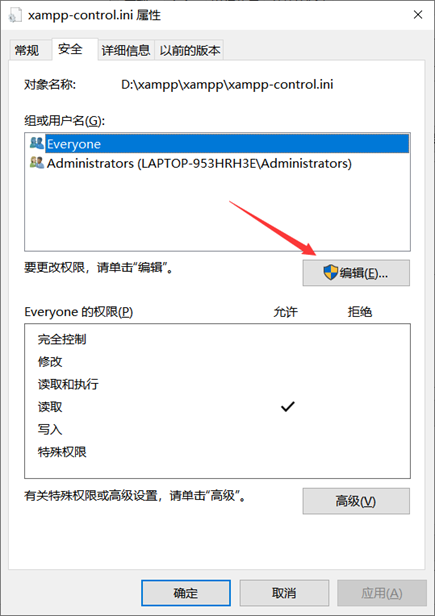
点击添加，再点击高级，最后点击查找，选中管理员权限的那个单人图标，点击确定。

然后勾选完全控制，点击确定

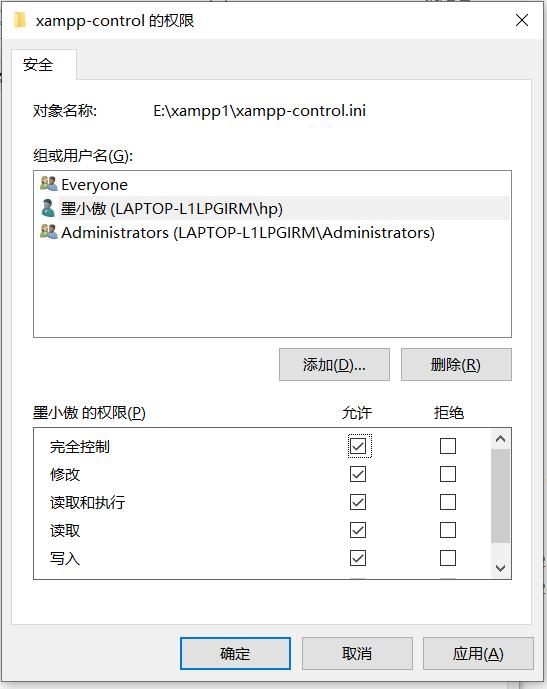
然后返回xampp页面，打开Conflg修改端口保存时就不会被拒绝访问了。

2.下载安装pikachu

下载地点：https://github.com/zhuifengshaonianhanlu/pikachu

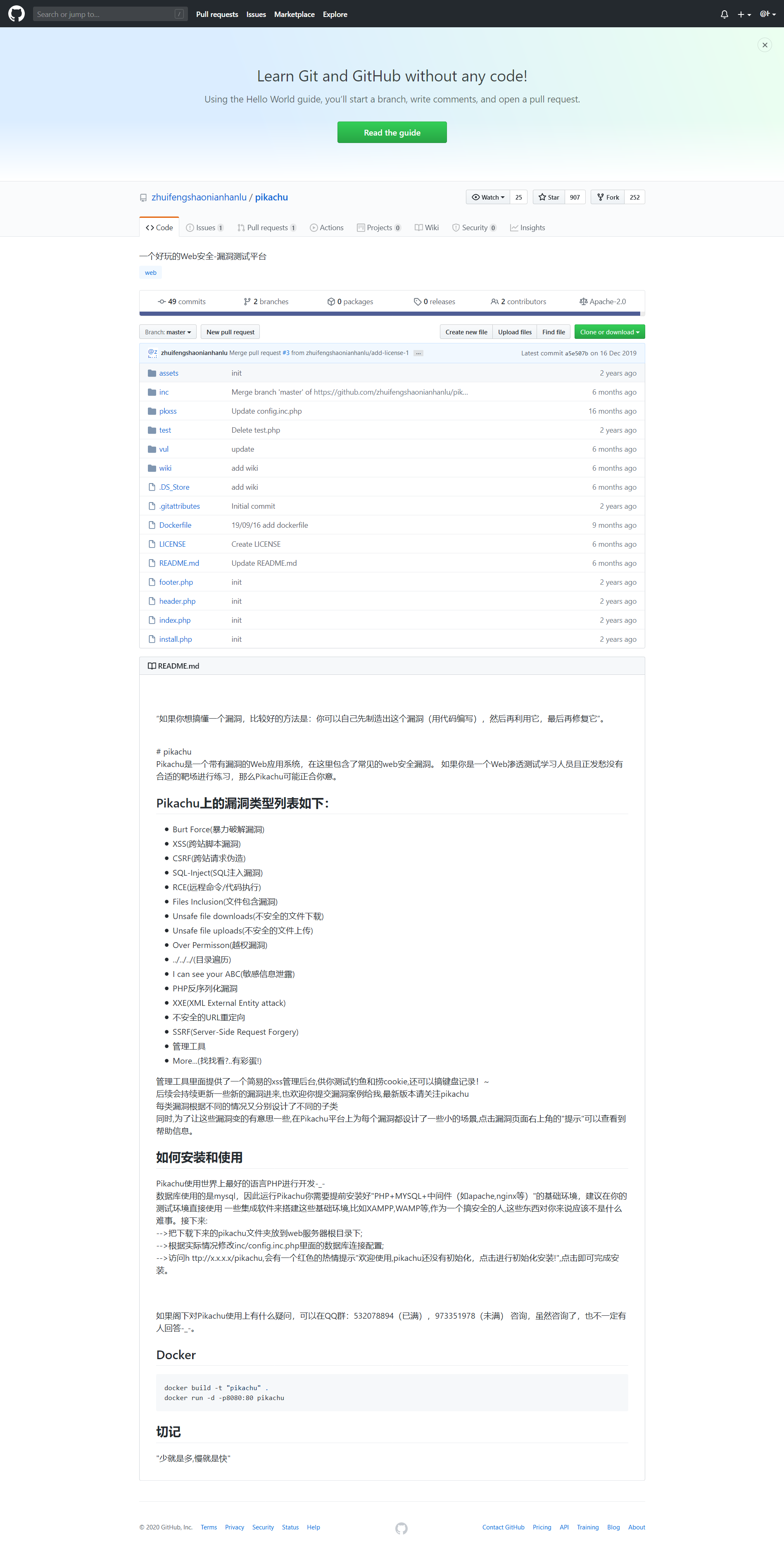
选择Clone or download，点击Download ZIP下载软件压缩包。

将下号pikachu压缩包解压到xampp文件夹的htdocs文件中

这时pikachu还需要进行文件配置的修改才能连上数据库，打开pikachu文件夹中的inc，

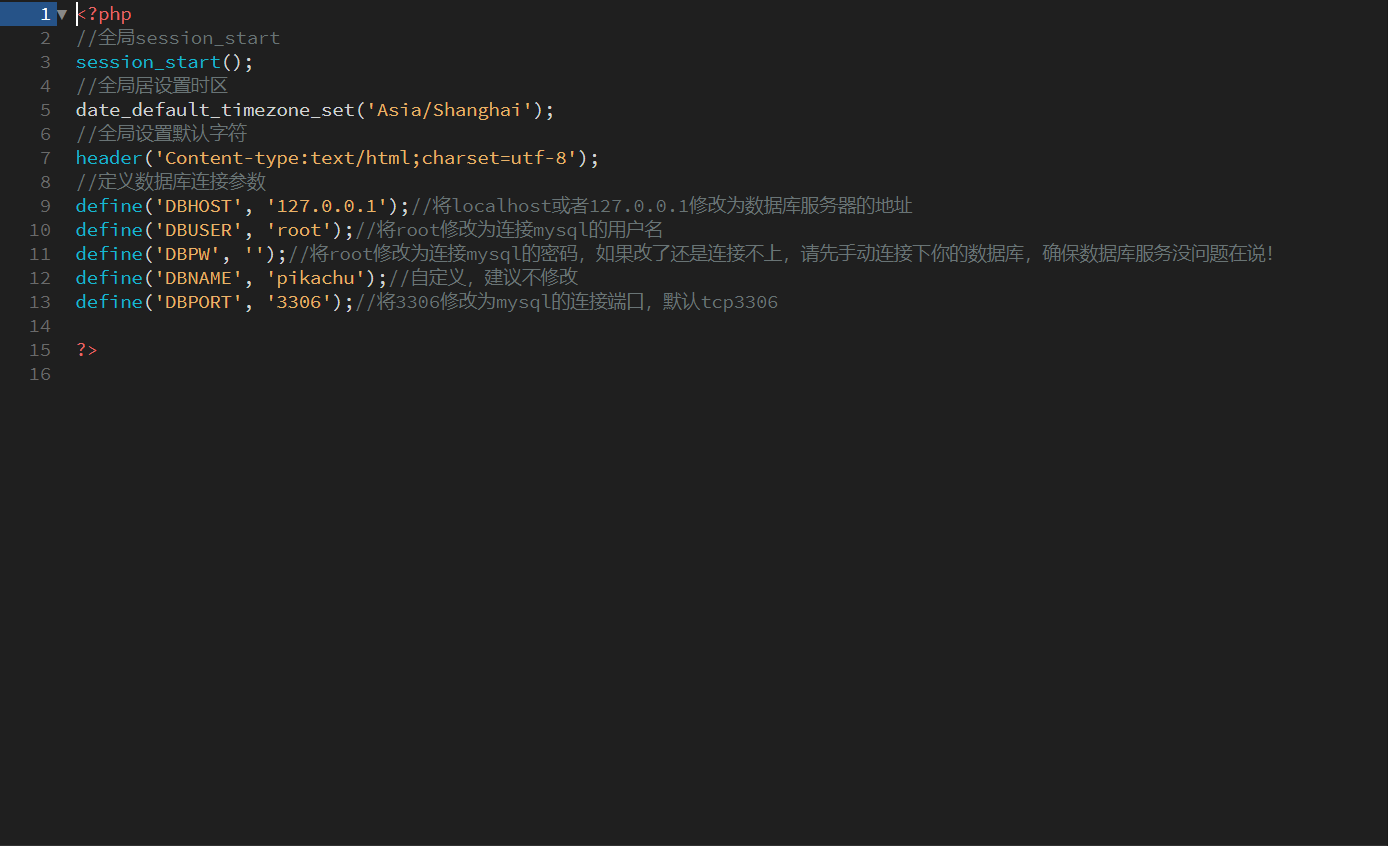
打开config.inc.php文件，这是一个PHP文件，如果打不开，可以下载一个Notepad++软件，账户和密码可以自定义，设置完毕后保存关闭。

再打开maxpp软件，点击MySQL的Admin

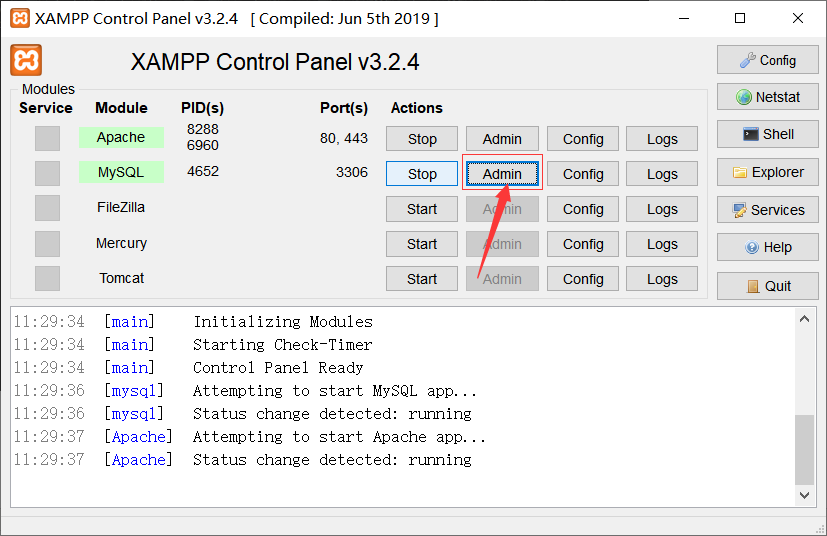
点击账户

点击127.0.0.1或localhost的修改权限

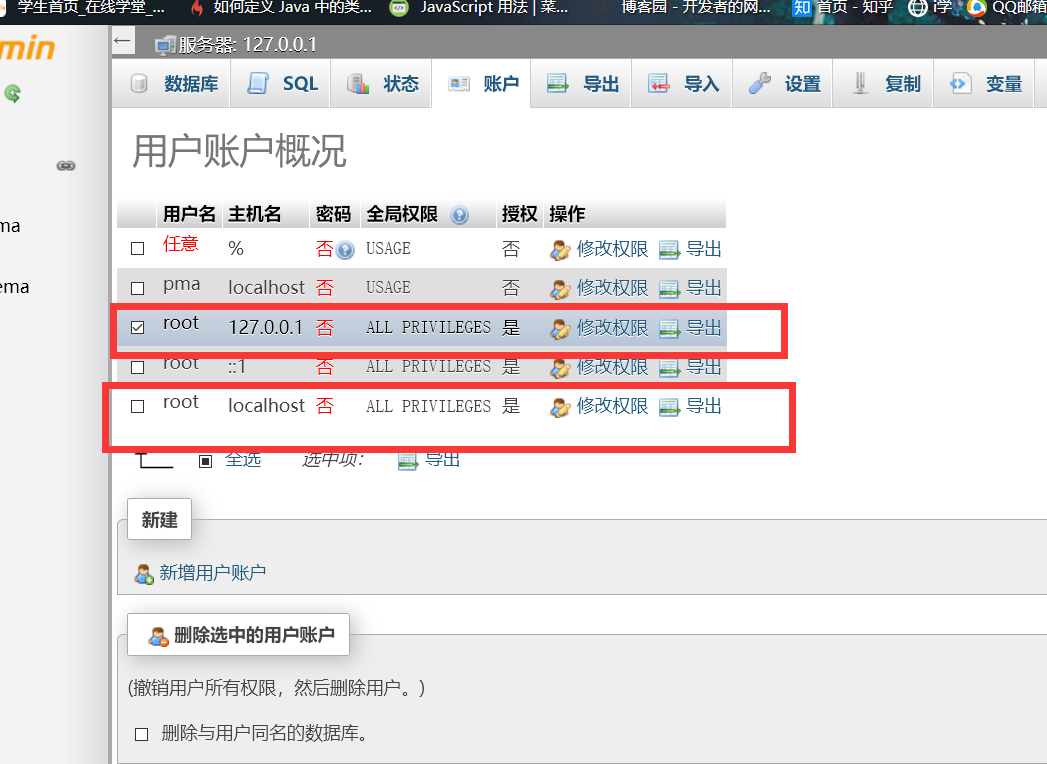
点击修改密码，

若在pikachu的config.inc.php文件中自定义了账号密码，只需将自定义的账号密码输入进去即可，然后执行保存。

4.登入pikachu平台

如果是默认端口只需在浏览器的地址栏输入http://127.0.0.1/pikachu/即可进入

若因Apache端口冲突等问题修改过Apache端口，则输入http：//127.0.0.1：自定义端口/pikachu/

例如上面我将Apache端口80改为了801 所以我进入pikachu平台的网址就变成了http：//127.0.0.1:801/pikachu/

成功进入平台之后，点击红色字体进行初始化，即可开始学习了