数据结构之DFS与BFS

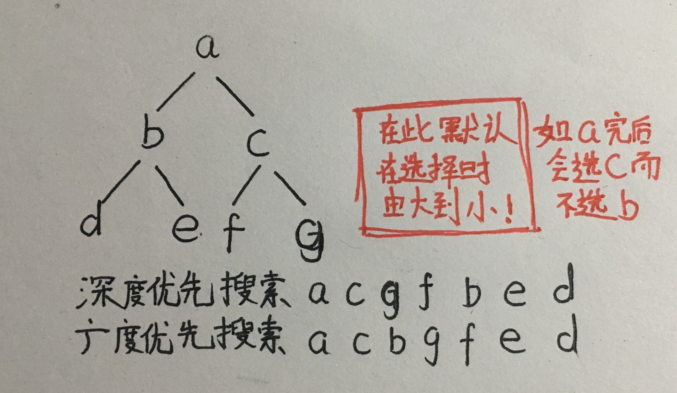
深度搜索（DFS） and  广度搜索（BFS）

代码如下:

 #include "stdafx.h"
 #include<iostream>
 #include<string>
 using namespace std;
 #define MAX 30
 #define MVNum 100
 #define ERROR 1
 typedef char VerTexType;
 typedef int Status;
 typedef int QElemType;
 #define MAXSIZE 100
 #define OK 1
 #define ERROR 0
 #define OVERFLOW -2
 typedef struct ArcNode                 //边结点
 {
     int adjvex;                        //改变所指向的顶点的位置
     struct ArcNode *nextarc;           //指向下一条边的指针
     string info;                       //和边相关的信息
 }ArcNode;
 typedef struct VNode                   //顶点信息
 {
     VerTexType data;
     struct ArcNode *link;              //指向第一条依附该顶点的边的指针
 }VNode;                                //AdList表示邻接表类型
 typedef struct                         //邻接表
 {
     VNode xlist[MAX];
     int vexnum, arcnum;                //图的当前顶点数和边数
 }ALGraph;

 typedef struct Node                    //构造队列
 {
     int data;
     struct Node *next;
 }Node,*QNode;
 typedef struct
 {
     QNode front;                       //队头指针
     QNode rear;                        //对尾指针
 }Queue;
 Status InitQueue(Queue &Q)             //初始化队列
 {
     Q.front = Q.rear=new Node;         //生成新节点作为头节点，对头和队尾指针指向此节点
     if (!Q.front)
         exit(OVERFLOW);
     Q.front->next = NULL;               //头结点的指针域置空
     return OK;
 }

 Status EnQueue(Queue &Q, int e)        //入队操作
 {
     QNode p = new Node;
     if (!p)                            //存储分配失败
         exit(OVERFLOW);
     p->data = e;
     p->next = NULL;
     Q.rear->next = p;
     Q.rear = p;                        //把当前的p设置尾对尾节点，rear指向p
     return OK;
 }

 Status DeQueue(Queue &Q, int &e)       //出队操作
 {
     QNode p;
     p = Q.front->next;                 //将欲删除的对头结点暂存给p
     Q.front->next = p->next;           //将原队头节点后继p->next赋值给头结点后继
     if (Q.rear == p)                   //如果队头是队尾，则删除后将rear指向头节点
         Q.rear = Q.front;
     e = p->data;                       //将欲删除的对接点赋值给e
     delete p;
     return OK;
 }

 Status QueueEmpty(Queue Q)             //队列判空
 {
     if (Q.rear == Q.front)
         return ;
     else
         return ;
 }

 int LocateVex(ALGraph &G, char &v)     //定位函数
 {
     int i;
     for (i = ; i < G.vexnum; i++)
     {
         if (G.xlist[i].data == v)
             return i;
     }
     if (i >= G.vexnum)
         return ERROR;
     else
         return ;
 }
 void CreateUDG(ALGraph &G)             //创建无向图
 {
     ArcNode *p1, *p2;
     int i, j, k;
     char v1, v2;
     cout << "请输入图的顶点数、边数：" << endl;
     cin >> G.vexnum >> G.arcnum;       //输入总顶点数，总边数
     cout << "请输入顶点的值:(顶点之间用空格分离)" << endl;
     for (i = ; i < G.vexnum; i++)
     {
         cin >> G.xlist[i].data;        //输入顶点值
         G.xlist[i].link = NULL;        //初始化表头结点的指针域为NULL
     }
     cout << "请输入弧尾和弧头：" << endl;
     for (k = ; k < G.arcnum; k++)
     {
         cin >> v1 >> v2;               //输入各边，构造邻接表
         i = LocateVex(G, v1);
         j = LocateVex(G, v2);
         p1 = new ArcNode;              //生成一个新结点*p1
         p1->adjvex = j;                //邻接点序号为j
         p1->nextarc = G.xlist[i].link;
         G.xlist[i].link = p1;
         p2 = new ArcNode;
         p2->adjvex = i;
         p2->nextarc = G.xlist[j].link;
         G.xlist[j].link = p2;
     }
     cout << "图构建成功！" << endl<<endl;
 }

 static bool visited[MAX];              //访问过visited，为1否则为0

 void DFS(ALGraph G, int m)             //深度优先搜索
 {
     visited[m] = true;                 //标记已经遍历过
     cout << G.xlist[m].data<<" ";
     ArcNode *p = G.xlist[m].link;
     while (p)
     {
         if (!visited[p->adjvex])
             DFS(G, p->adjvex);
         p = p->nextarc;
     }
 }

 void BFS(ALGraph G,int n)              //广度优先搜索
 {
     ArcNode *p;
     Queue Q;
     for (int i = ; i < G.vexnum; i++)
         visited[i] = false;
     InitQueue(Q);
     for (int i = ; i < G.vexnum; i++)
     {
         if (!visited[i])
         {
             visited[i] = true;
             cout << G.xlist[i].data<<" ";
             EnQueue(Q, i);
             while (!QueueEmpty(Q))
             {
                 DeQueue(Q, i);
                 p = G.xlist[i].link;   //找到当前顶点编表链表头指针
                 while (p)
                 {
                     if (!visited[p->adjvex])//若此顶点未访问
                     {
                         visited[p->adjvex] = true;
                         cout << G.xlist[p->adjvex].data<<" ";
                         EnQueue(Q, p->adjvex);//将此顶点入队列
                     }
                     p = p->nextarc;    //指针指向下一个邻接点
                 }
             }
         }
     }
 }

 void coutGraphD(ALGraph G)             //深搜输出函数
 {
     for (int i = ; i < G.vexnum; i++)
         visited[i] = false;
     cout << "深度优先搜索输出的顶点的结果为:" << endl;
     for (int i = ; i < G.vexnum; i++)
         if (!visited[i])
             DFS(G, i);
     cout << endl;
 }
 void coutGraphW(ALGraph G)             //广搜输出函数
 {
     for (int i = ; i < G.vexnum; i++)
         visited[i] = false;
     cout << "广度优先搜索输出的顶点的结果为:" << endl;
     for (int i = ; i < G.vexnum; i++)
         if (!visited[i])
             BFS(G, i);
     cout << endl;

 }
 int main()
 {
     ALGraph MG;
     CreateUDG(MG);
     coutGraphD(MG);
     coutGraphW(MG);
     return ;
 }

运行结果：