Lucas 大组合数

题目：HDU 3037

题意：有n个树，m个坚果，放到n个树里，可以不放完，有多少种方法。

分析：

得到组合数了。

大组合数什么费马小定理，Lucas定理都来了；

总的说，不能用二维地推了，用的却是组合数的定义。

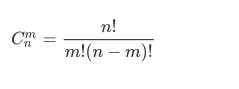
一般来说大组合通常要取模。

那么不能边乘边模，边除边模，等式不会成立。

根据逆元，除以一个数取模 = 乘以这个数对mod的逆元。

那么式子就可以写成：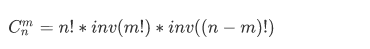

这里，我们可以预处理所有 i 对 mod 的逆元后，累乘，这样得到的就是阶乘的逆元。

然后就是求 i 对 mod 的逆元了，什么扩展欧几里得就来了。

当然，有费马小定理。

inv[i] = (mod-mod/i)*inv[mod%i]%mod；

整个求大组合数就是这样出来了。

void init() {

    fac[] = ;
    for(int i=;i<maxn;i++)
        fac[i] = i*fac[i-]%mod;

    inv[] = inv[] = ;
    for(int i=;i<maxn;i++)
        inv[i] = (ll)(mod-mod/i)*inv[mod%i]%mod;

    for(int i=;i<maxn;i++)
        inv[i] = inv[i-]*inv[i]%mod;

}

ll C(ll n,ll m) {

    if(n<m)
        return ;
    return fac[n]*inv[m]%mod*inv[n-m]%mod;

}

但是这个题目n,m的范围惊人1000000000，作为阶乘，逆元，数组开不下。

Lucas来了：

看结果吧：

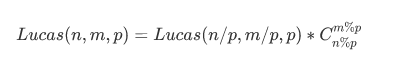
还是有组合数，用了费马定理：

fac[n]*Inv(fac[m])%P*Inv(fac[n-m])%P；

因为这里的对P的逆元 Inv已经不能用数组表示和地推了，Inv()函数，利用了费马定理，快速幂等等，原理很复杂了，哈哈~~~，我就不证明了。

void initFac(int n) {
    fac[] = ;
    for(int i=;i<=n;i++)
        fac[i] = i*fac[i-]%P;
}

ll Pow(ll a,int b) {
    ll re = ;
    for(;b;b>>=,a=a*a%P)
        if(b&) re = re*a%P;
    return re;
}

ll Inv(ll a) {
    return Pow(a,P-);
}

ll C(ll n,ll m) {
    if(n<m) return ;
    return fac[n]*Inv(fac[m])%P*Inv(fac[n-m])%P;
}

ll Lucas(ll n,ll m) {
    if(n<m) return ;
    ll re = ;
    for(;m;n/=P,m/=P)
        re = re*C(n%P,m%P)%P;
    return re;
}