[xsy2363]树

设$f_{i,j}$表示$i$个点的树，权值为$j$且可以不选根的方案数，$g_{i,j}$表示$i$个点的树，权值为$j$且必选根的方案数

首先$g_{1,1}=0$

我们可以把原树连上一个新的子树，转移有四种情况，其中黑点表示原来在最大独立集中的点

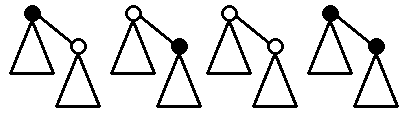
$\begin{align*}g_{i,j}&\leftarrow\sum\limits_{a=1}^{i-1}\sum\limits_{b=1}^{j-1}g_{i-a,j-b}f_{a,b}\\f_{i,j}&\leftarrow\sum\limits_{a=1}^{i-1}\sum\limits_{b=1}^{j-1}f_{i-a,j-b}g_{a,b}\\f_{i,j}&\leftarrow\sum\limits_{a=1}^{i-1}\sum\limits_{b=1}^{j-1}f_{i-a,j-b}f_{a,b}\\f_{i,j-1}&\leftarrow\sum\limits_{a=1}^{i-1}\sum\limits_{b=1}^{j-1}g_{i-a,j-b}g_{a,b}\end{align*}$

最后一条是因为两个原来在最大独立集中的点相邻，我们要削除一个点

注意到转移是卷积的形式，设$G_{i}(x)$为$g_{i,1\cdots n}$的生成函数，$F_i(x)$为$f_{i,1\cdots n}$的生成函数，我们有$\begin{align*}G_i(x)=\sum\limits_{a=1}^{i-1}G_{i-a}(x)F_a(x),F_i(x)=\sum\limits_{a=1}^{i-1}F_{i-a}(x)F_a(x)+F_{i-a}(x)G_a(x)+\dfrac{G_{i-a}(x)G_a(x)}x\end{align*}$

可以直接对$f_{1,1\cdots n}$和$g_{1,1\cdots n}$DFT后用点值计算$G_{2\cdots n}$和$F_{2\cdots n}$，最后再IDFT回来

这题是不是可以暴力DFT啊23333

#include<stdio.h>
typedef long long ll;
const int mod=998244353;
ll mul(ll a,ll b){return a*b%mod;}
ll ad(ll a,ll b){return(a+b)%mod;}
ll de(ll a,ll b){return(a-b)%mod;}
ll pow(ll a,ll b){
	ll s=1;
	while(b){
		if(b&1)s=mul(s,a);
		a=mul(a,a);
		b>>=1;
	}
	return s;
}
int rev[512],N,iN;
void pre(int n){
	int i,k;
	for(N=1,k=0;N<n;N<<=1)k++;
	for(i=0;i<N;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(k-1));
	iN=pow(N,mod-2);
}
void swap(ll&a,ll&b){a^=b^=a^=b;}
void ntt(ll*a,int on){
	int i,j,k,t,w,wn;
	for(i=0;i<N;i++){
		if(i<rev[i])swap(a[i],a[rev[i]]);
	}
	for(i=2;i<=N;i<<=1){
		wn=pow(3,(on==1)?(mod-1)/i:(mod-1-(mod-1)/i));
		for(j=0;j<N;j+=i){
			w=1;
			for(k=0;k<i>>1;k++){
				t=mul(w,a[i/2+j+k]);
				a[i/2+j+k]=de(a[j+k],t);
				a[j+k]=ad(a[j+k],t);
				w=mul(w,wn);
			}
		}
	}
	if(on==-1){
		for(i=0;i<N;i++)a[i]=mul(a[i],iN);
	}
}
ll f[510][512],g[510][512],inv[512];
int main(){
	int n,i,j,k;
	scanf("%d",&n);
	pre(n);
	j=pow(3,mod-1-(mod-1)/N);
	k=1;
	for(i=0;i<N;i++){
		inv[i]=k;
		k=mul(j,k);
	}
	g[1][1]=1;
	ntt(f[1],1);
	ntt(g[1],1);
	for(i=2;i<=n;i++){
		for(j=1;j<i;j++){
			for(k=0;k<N;k++){
				f[i][k]=(f[i][k]+f[i-j][k]*f[j][k]+f[i-j][k]*g[j][k]+mul(g[i-j][k],g[j][k])*inv[k])%mod;
				g[i][k]=(g[i][k]+g[i-j][k]*f[j][k])%mod;
			}
		}
	}
	for(i=1;i<=n;i++){
		for(j=0;j<N;j++)f[i][j]=ad(f[i][j],g[i][j]);
		ntt(f[i],-1);
		for(j=0;j<=n;j++)printf("%lld ",(f[i][j]+mod)%mod);
		putchar('\n');
	}
}