《DirectX 9.0 3D游戏开发编程基础》第二章绘制流水线读书笔记

模型的表示

场景：物品或模型的集合

任何物品都可以用三角形网络逼近表示。我们经常用以下术语描述三角形网络：多边形(polygons)、图元(primitives)、网络几何单元(mesh geometry)。

描述三角形：指定三个顶点

描述物品：三角形单元列表

顶点格式

可以创建我们所希望包含的顶点信息，如位置，颜色等，如下所示

Code Snippet

struct ColorVertex{
float _x,_y,_z;
DWORD color;
};
struct NormalTexVertex{
float _x,_y,_z;
float _nx,_ny,_nz;
float _u,_v;
};

顶点结构定义好之后，就需要用灵活顶点格式(FVF)标记组合来描述顶点的组织结构。如下所示

#define FVF_COLOR (D3DFVF_XYZ | DEDFVF_DIFFUSE) //包含了位置信息和漫反射信息

#define FVF_NORMAL_TEX (D3DFVF_XYZ | D3dFVF_NORMAL | D3DFVF_TEX1) //包含了位置、法线、纹理坐标。

灵活顶点格式约定：标记指定顺序与顶点结构中相应类型数据保持一致

三角形单元

三角形单元包含了我们所希望绘制的每个独立三角形的数据。如下图所示产，并指定每个三角形单元的顶点。

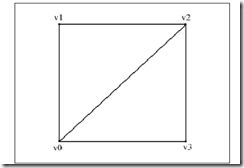
Vertex rect[6] = {v0,v1,v2,v0,v2,v3}

索引

原理：顶点列表包含了全部独立的顶点，索引包含了指向顶点列表的索引，这些索引规定了为构建三角形单元，各顶点应按何种方式来组织。上图中的例子可以这样创建

Vertex vertexList[4] = {v0,v1,v2,v3}

WORD indexList[6] = {0,1,2,0,2,3} //其中0,1,2 都上vertexlist的下标。

虚拟摄像机

那些位于视域体之外的物品是不可见的，在进一步处理时就应将其丢弃。丢弃这类数据运算过程称为裁剪。

绘制流水线

定义：建立了3d场景的几何描述，并设置好虚拟摄像机，我们下面的任务就是在显示器中建立该场景的2d表示。为了实现这一目标实施的一系列去算统称为绘制流水线

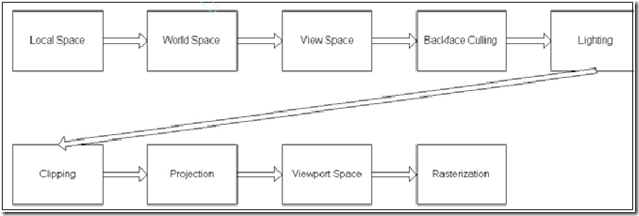
DirectX坐标变换：IDirect3DDevice9->SetTransform（变换类型,变换矩阵）。例如为了实现自局部坐标系到世界坐标系的变换，我们可以这样写

Device->SetTransform(D3DTS_WORD, & worldMatrix)

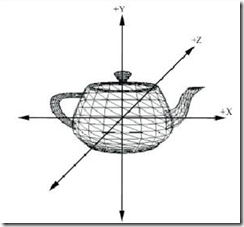
局部坐标系:、

定义：用于定义构成物品三角形列表的坐标系。如下图是在自身坐标系中定义的茶壶

世界坐标系

位于局部坐标系中的物品通过一个称为世界变换的去算过程到世界坐标系。通常包括平移、旋转等。

假如我们想让一个立方体位于世界坐标系中的点(-3,2,6)上，让一个球体位于(5,2,-1) 上，可以如下实现

Code Snippet

D3DMATRIX cubeWorldMatrix;
D3DXMatrixTranslation(&cubeWorldMatrix,-3.0f,2.0f,6.0f);
D3DXMATRIX sphereWorldMatrix;
D3DXMatrixTranslation(&sphereWorldMatrix,5,0f,0.0f,-2.0f);
//set the cub's transformation
Device->SetTransform(D3DTS_WORLD,&cubeWorldMatrix);
drawCube();
Device->SetTransform(D3DTS_WORLD,&sphereWorldMatrix);
drawSphere();

观察坐标系

为简化运算将摄像机变换至至世界坐标系原点，并使其光阵与z轴同向。同时空间中的所有几何体都随着摄像机一同进行变换，以保证摄像机视场恒定。这种变换称为取景变换。我们称变换后的几何体位于观察坐标系中。

取景变换矩阵可以用如下函数得到

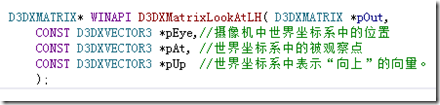
假如摄像机们于（5,3,10），其观察点为世界坐标系原点。我们可以这样创建取景变换矩阵

Code Snippet

D3DXVECTOR3 position(5.0f,3.0f,-10.0f);
D3DXVECTOR3 targetPoint(0.0f,0.0f,0.0f);
D3DXVECTOR3 worldUp(0.0f,1.0f,0.0f);
D3DXMATRIX V;
D3DXMatrixLookAtLH(&V,&position,&targetPoint,&worldUp);

取景变换需要用IDirect3DDevice9:: SetTransform来设定，其中用于变换的类参数需要指定为D3DTS_VIEW;

Device->SetTransform(D3DTS_VIEW,&V)

背面消隐

通俗来讲就是看不见物体的背面，我们将背面加以剔除，这称为背面消隐。

哪些是背面朝向：默认状态下Dirct3d认为顶点顺时针（观察坐标系中）的三角形单元是正面朝向的。顶点排列顺序为逆时针的是背面朝向的

如果某些原因导致背面消隐方式不能满足应用要求，我们可以修改绘制状态来达到目的

Devoce->SetRenderState(D3DRS_CULLMODE,Value)

其中 Value可取以下值：D3DCULL_NONE 完全禁用背面消隐。 D3DCULL_CW 只用顺时针绕序的三角形进行消隐。 D3DCULL_CCW 默认值。

光照

裁剪

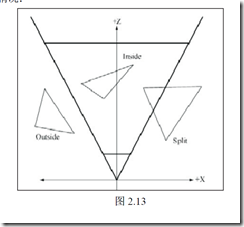
投影

观察坐标系中我们的任务是获取3d场景的2d表示。从n维变为n-1维的过程称为投影。实现投影有多多种方式，我们只对其中一种感兴趣，即透视投影。透视投影会产生“透视缩短”的效果，即近大远小。我们将使用以下函数其功能是依据视域体的描述信息创建一个投影矩阵。

视口变换

定义：将顶点坐标从投影窗口投影窗口转换到屏幕的一个矩形区域中。

光栅化

为了绘制每一个三形单元，如何计算构成三角形单元的每个像素的颜色值。