1326. 灌溉花园的最少水龙头数目 (Hard)

问题描述

1326. 灌溉花园的最少水龙头数目 (Hard)

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, ..., n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i]

（下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方，请你返回 -1 。

示例 1：

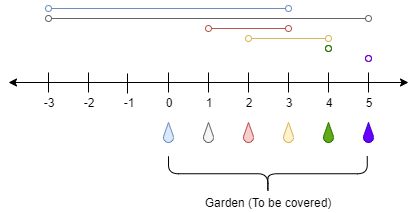
输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。

示例 2：

输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。

提示：

• 1 <= n <= 10⁴
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

解题思路

贪心

假设当前能浇灌的最右端为end，对应的水龙头为start_idx，那么应该选满足start[i] <= end且end[i]最大的i。在这里，我们构建一个数组vector<int> right_most(n + 1, 0)，表示当坐标i的点能被浇灌到时，所能浇灌到的最远点。

然后，我们从0~n遍历i，如果right_most[i]大于next_right，那么更新next_right，原先的next_right记为cur_right，如果i == cur_right了，说明要再开一个水龙头。

排序+二分查找

这个做法也是有一点贪心的思路，假设当前能浇灌的最右端为end，对应的水龙头为start_idx，那么应该选满足start[i] <= end且end[i]最大的i，可以利用二分查找找到满足start[i] <= end的i的最大值idx，然后遍历[start_idx, idx]，找最大的end[i],并更新start_idx。

动态规划

dp[i]表示覆盖[0, i]所需要的最少水龙头数量；

我们假设dp[i]的情况下，打开的最后一个水龙头为(start[j], end[j])，那么对于start[j] < k < end[j]，dp[k] = min(dp[k], dp[start[j]] + 1)，所以这里我们需要将dp[i]初始化为一个极大值，并且需要将water_range数组按照start[i]从小到大排序。

代码

动态规划

class Solution {
  public:
    int minTaps(int n, vector<int> &ranges) {
        vector<vector<int>> water_range;
        for (int i = 0; i <= n; i++) {
            water_range.push_back({std::max(0, i - ranges[i]), std::min(i + ranges[i], n)});
        }
        std::sort(water_range.begin(), water_range.end());
        vector<int> dp(n + 1, 30000);
        dp[0] = 0;
        for(int i = 0; i <= n; i++) {
            if (dp[water_range[i][0]] == 30000)
                return -1;
            for (int j = water_range[i][0]; j <= water_range[i][1]; j++) {
                dp[j] = std::min(dp[j], dp[water_range[i][0]] + 1);
            }
        }
        return dp[n];
    }
};

贪心

class Solution {
public:
    int minTaps(int n, vector<int> &ranges) {
        int right_most[n + 1]; memset(right_most, 0, sizeof(right_most));
        for (int i = 0; i <= n; ++i) {
            int r = ranges[i];
            if (i > r) right_most[i - r] = i + r; // 对于 i-r 来说，i+r 必然是它目前的最大值
            else right_most[0] = max(right_most[0], i + r);
        }

        int ans = 0;
        int cur_right = 0; // 已建造的桥的右端点
        int next_right = 0; // 下一座桥的右端点的最大值
        for (int i = 0; i < n; ++i) { // 注意这里没有遍历到 n，因为它已经是终点了
            next_right = max(next_right, right_most[i]);

            if (i == cur_right) { // 到达已建造的桥的右端点
                if (i == next_right) return -1; // 无论怎么造桥，都无法从 i 到 i+1
                cur_right = next_right; // 造一座桥
                ++ans;
            }
        }
        return ans;
    }
};

排序+二分查找

class Solution {
  public:
    // 二分查找
    int Bfind(vector<vector<int>> &vec, int target, int start_idx) {
        int left = start_idx, right = vec.size();
        int mid = left + (right - left) / 2;
        while (left < right) {
            if (vec[mid][0] < target) {
                left = mid + 1;
            } else {
                right = mid;
            }
            mid = left + (right - left) / 2;
        }
        return left;
    }
    int minTaps(int n, vector<int> &ranges) {
        vector<vector<int>> water_range;
        for (int i = 0; i <= n; i++) {
            water_range.push_back({i - ranges[i], i + ranges[i]});
        }
        auto cmp = [&](vector<int> &v1, vector<int> &v2) {
            if (v1[0] == v2[0])
                return v1[1] <= v2[1];
            return v1[0] < v2[0];
        };
        std::sort(water_range.begin(), water_range.end(), cmp);
        int start_idx = 0, end = 0;
        int cnt = 0;
        while (end < n) {
            int idx = Bfind(water_range, end + 1, start_idx) - 1; // 找到满足start[idx] <= end的最大的idx
            for (int i = start_idx; i <= idx; i++) {
                if (water_range[i][1] > end) {
                    start_idx = i;
                    end = water_range[i][1];
                }
            }
            cnt++;
            if (cnt > n)
                return -1;
        }
        return cnt;
    }
};