[数据结构]普里姆（Prim）算法生成最小生成树

前提介绍：最小生成树概念

　　一个连通图的生成树是图的极小连通子图，它包含图中的所有定点，并且只含尽可能少的边，这意味着对于生成树来说，就砍去使生成树变成非连通图；若给它怎家一条边就会形成图中的一条回路。

　　对于一个带权连通无向图G=(V,E)，生成树不同，每个树的权也可能不同。设W为G的所有生成树的集合，若T为G中边的权值之和最小的那棵生成树，则T成为G的最小生成树。

Prim算法概念

　　Prim算法的执行非常类似于寻找图的最短路径的Dijkstra算法。假设N={V,E}是连通网，Et是N上最小生成树中边的集合。算法从Vt={u0}（u0∈V），Et={}开始，重复执行下述操作：在所有u∈Vt，v∈V-Vt的边（u，v）∈E中找一条代价最小的边(u0,v0)并加入集合Et，同时将v0并入Vt，直到Vt=V为止。此时Et中必有n-1条边，则T={Vt，Et}为N的最小生成树。

　　Prim算分的步骤如下：

　　初始化：向空树T=（Vt，Et）中添加图G=（V,E）的任一定点u0，使Vt={u0}，Et=空集；

　　循环下述操作：从图G中选择满足{（u，v）|u∈Vt，v∈V-Vt}且具有最小权值的边（u，v），并置Vt=Vt∪{v}，Et=Et∪{（u，v）}。

实例及解析

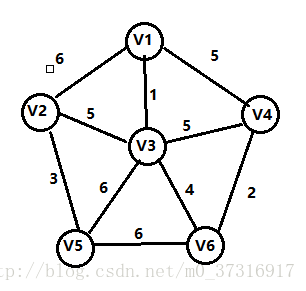
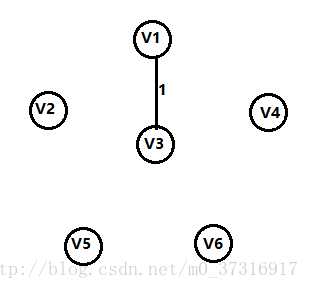
　　第一步：

从图中选择一条最短的边加入集合，不难看出，1是此时最短的边。

第二步：



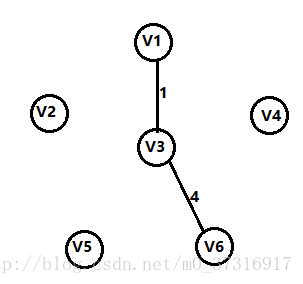
此时我们可以从V1,V2两个顶点出发，寻找下一个定点与这两个顶点之一相连，并且能使相连的這条边是最短的，所以我们下一个选择的是V6，此时顶点集合有：V1,V3,V6。

第三步：



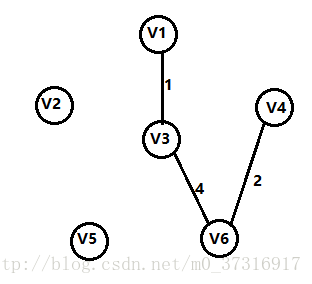
从V1,V3,V6三个顶点出发，我们要寻找下一条最短的边，不难发现，此时2是最短的那一条边，连接V6,V4，所以把它加入边的集合（要注意，加入的边不能使生成树带有回路！），此时顶点集合:v1,v3,v4,v6

第四步：



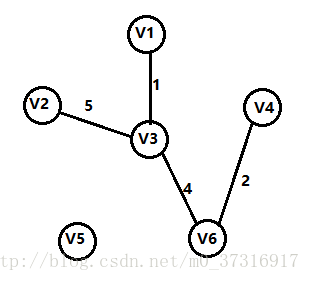
从V1,V3,V6,V4四个顶点出发，寻找下一条最短的边并且不能使生成树带有回路，此时可以发现，V3到V2的5是最短的这条边。

第五步：



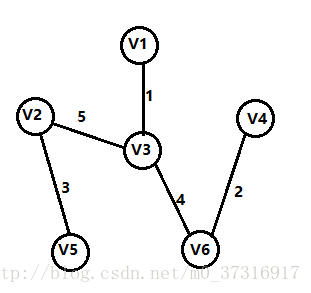
最后一步，从V1,V2,V3,V6,V4的顶点出发，寻找吓下一条最短的边，并且不能形成回路，很明显V2到V5这条边最短，加入之后最小生成树已经形成。

伪代码实现

void Prim(G,T){
    T=空集;//初始化空树
    U={w}；//添加任一顶点）
    while（（V-U）！=空集）{
    设（u，v）是使u∈U与v∈（V-U），且权值最小的边;
    T=T∪（u，v）;  //边归入树
    U=U∪{v};  //顶点归入输
    }
}

算法的复杂度

　　Prim算法的时间复杂度为O（|V|²），不依赖于|E|，因此它很适合于求解边稠密的图的最小生成树，虽然采用其他办法可以改进Prim算法的时间复杂度，但增加了实现的复杂性。