GBDT初识

GBDT的决策树：

​ 无论是处理回归任务还是二分类以及多分类任务，GBDT使用的决策树是CART回归树。因为GBDT每次迭代要拟合的是梯度值，是连续值所以要用回归树。

​ 对于回归树算法来说最重要的是寻找最佳的划分点，那么回归树中的可划分点包含了所有特征的所有可取的值。在分类树中最佳划分点的判别标准是熵或者基尼系数，都是用纯度来衡量的，但是在回归树中的样本标签是连续数值，所以再使用熵之类的指标不再合适，取而代之的是平方误差，它能很好的评判拟合程度。

注意：

• 梯度下降从来都是拟合负梯度，GBDT平方损失只是恰好等于残差

• 训练步骤：

  • 每棵决策树利用负梯度对样本点进行划分（拟合负梯度）
  • 求使得损失函数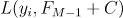最小的C（即树叶子结点的输出），且C的值通常是一个与负梯度相关的式子（见下文分类问题模块介绍）

提升树（Boosting Tree）

​ 先来个通俗理解：假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。最后将每次拟合的岁数加起来便是模型输出的结果。

Gradient Boosting：拟合负梯度

​ 当损失函数是平方损失和指数损失函数时，提升树（Boosting Tree）每一步优化是很简单的，但是对于一般损失函数而言，往往每一步优化起来不那么容易，针对这一问题，Freidman提出了梯度提升树算法，这是利用最速下降的近似方法，其关键是利用损失函数的负梯度作为提升树算法中的残差的近似值。

​ Gradient Boosting 的基本思想是：串行地生成多个弱学习器，每个弱学习器的目标是拟合先前累加模型的损失函数的负梯度， 使加上该弱学习器后的累积模型损失往负梯度的方向减少。即如果第 m 轮弱学习器拟合损失函数关于累积模型 的负梯度，则加上该弱学习器之后累积模型的 loss 会最小。（个人理解是：随着m棵树的不断叠加使得模型的整体梯度趋近于0，模型近似最优）

GBDT算法原理

• GBDT是CART决策树与Gradient Boosting的组合体。
• GBDT的简易实现版本

GBDT 回归与分类

• GBDT（Gradient Boosting Decision Tree）是弱学习器使用 CART 回归树的一种 Gradient Boosting，使用决策树作为弱学习器的一个好处是：决策树本身是一种不稳定的学习器（训练数据的一点波动可能给结果带来较大的影响），从统计学的角度单棵决策树的方差比较大。而在集成学习中，弱学习器间方差越大，弱学习器本身泛化性能越好，则集成学习模型的泛化性能就越好。因此使用决策树作为弱学习器通常比使用较稳定的弱学习器（如线性回归等）泛化性能更好。

• 回归问题

  GBDT 中的每个弱学习器都是 CART 回归树，在回归问题中，损失函数采用均方损失函数：
  
  
  
  损失函数的负梯度为：
  
  
  
  核心代码如下：

  def fit(self, train_X, train_y):
    self.estimator_list = list()
    self.F = np.zeros_like(train_y, dtype=float)
  
    for i in range(1, self.n_estimators + 1):
        # get negative gradients
        neg_grads = train_y - self.F
        base = DecisionTreeRegressor(max_depth=self.max_depth)
        base.fit(train_X, neg_grads)   # cart树的叶结点值是负梯度，也是残差
        train_preds = base.predict(train_X)
        self.estimator_list.append(base)
  
        if self.is_first:
            self.F = train_preds
            self.is_first = False
        else:
            self.F += self.lr * train_preds
  

• 分类问题

  GBDT 中都的弱学习器都是 CART 回归树，在回归问题上使用 GBDT 比较 intuitive，损失函数为均方损失，负梯度就是残差，下一棵树就去拟合之前的树的和与真实值的残差。对于分类问题，可以对拟合目标稍作转换实现分类。
  
  基本的思路可以参考线性回归通过对数几率转化为逻辑回归进行分类。逻辑回归也是广义上的线性模型，可以看做是线性回归模型去拟合对数几率
  
  
  
  
  
  
  
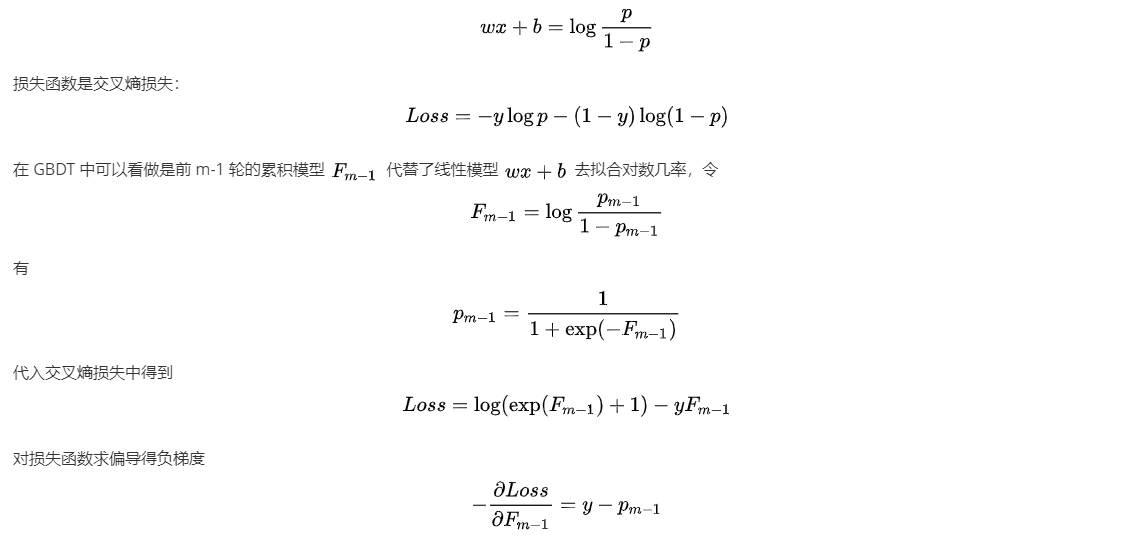
  可以看到最后的负梯度形式十分简洁，将此负梯度作为第 m 轮的拟合目标，依次不断迭代，GBDT 分类的核心代码如下：

  @staticmethod
  def logit(F):
     return 1.0 / (1.0 + np.exp(-F))
  
  def fit(self, train_X, train_y):
       self.estimator_list = list()
       self.F = np.zeros_like(train_y, dtype=float)
  
       for i in range(1, self.n_estimators + 1):
           # get negative gradients
           neg_grads = train_y - self.logit(self.F)
           base = DecisionTreeRegressor(max_depth=self.max_depth)
           base.fit(train_X, neg_grads)  #cart树的叶结点值是负梯度，不是实际标签的残差（个人理解，若有错误，请不吝指教）
           train_preds = base.predict(train_X)    # train_preds 即为C
           self.estimator_list.append(base)
  
           if self.is_first:
               self.F = train_preds
               self.is_first = False
           else:
               self.F += self.lr * train_preds
   ```
  
  

GBDT 优点和局限性

• 优点

1. 预测阶段速度快，树与树之间可以并行预测
2. 在数据分布稠密的数据上，泛化能力和表征能力都很好
3. 使用 CART 作为弱分类器不需要对数据进行特殊的预处理如归一化等

• 局限性

1. 在高维稀疏的数据上，表现不如 SVM 或神经网络
2. 训练过程需要串行训练，只能在决策树内部采用一些局部并行手段提高训练速度

参考链接：

• https://mp.weixin.qq.com/s/NBHF-se8UmDEGy9cKX_VQQ 包含实例展示
• https://zhuanlan.zhihu.com/p/64863699
• https://blog.csdn.net/kyle1314608/article/details/112602351 （重点参考）

小点

• 同一棵树中可以多次利用同一特征进行划分
  
  
• GBDT中会出现两棵树（除叶子结点外）结构相同的情况吗？
  • 学习率太小（把一棵树一次可以拟合好的树，让这棵树分多次来拟合）？