[algorithm] 汉诺塔问题

汉诺塔是根据一个传说形成的一个问题。汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

一、 问题

可以抽象为A、B、C三个柱子，A上从上向下串着半径从小大的不同的N个圆盘，将A上的圆盘移动到C上，但是一次只能从最顶端移动一个，小盘只能放在大盘上,问具体的走法？

1. 当 N=1时，直接 A->C上。

2. 当N=2时，B作为中转过渡，A->B,A->C，B->C . 三步走完。

3. 当N=N时,将塔座A的前n-1个盘子借助C盘（即目的盘）移到塔座B，移后，此时C为空座，那我们就可以将塔座A的第n个盘子移到塔座C了。接下来就将塔座B的n-1个盘子借助A移到塔座C，从而完成盘子的移动。

二、代码实现

/**
 * 汉诺塔问题：
 * <b>
 * 大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。
 * 大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
 * 并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
 * </b>
 * @author xwolf
 * @date 2017-05-26 10:25
 * @since 1.8
 */
public class HanoiTower {

    //总步数
    private static long total = 1L;

    /**
     * 具体走的流程
     * @param num  圆盘数量
     * @param start  起始柱子
     * @param middle 中间过渡柱子
     * @param end  结束(目标)柱子
     */
    public static void move(int num,String start,String middle,String end){
         if (num==1){
             System.out.println(String.format("第%d步,%d号盘从%s移动到%s: %s-->%s",total++,num,start,end,start,end));
         } else{

             move(num-1,start,end,middle);

             System.out.println(String.format("第%d步,%d号盘从%s移动到%s: %s-->%s",total++,num,start,end,start,end));

             move(num-1,middle,start,end);
         }
    }

    public static void main(String[] args) {
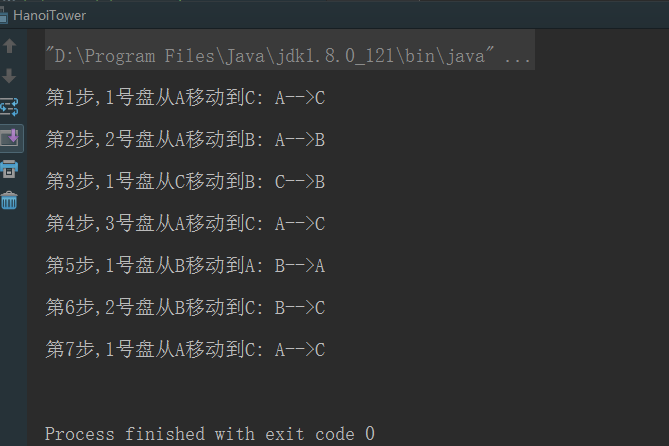
        move(3,"A","B","C");
    }
}