BZOJ 2820 YY的GCD

AC通道：http://www.lydsy.com/JudgeOnline/problem.php?id=2820

有种方法是枚举质数然后用BZOJ2301来做但是超时了...

具体式子大概张这样：

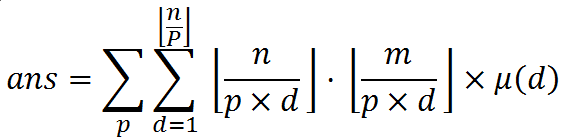
然后下面一步比较关键，就是将T=p*d带进去

这个时候需要读者自己先手化简一下将ans变成一个与T有关的式子

然后可以再看笔者这个式子

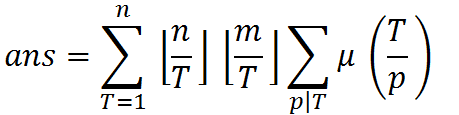
有几个注意的地方，首先T=p*d，所以T的范围是1...n

原式中的n/(p*d)和m/(p*d)就是(n/T)*(m/T)这个好懂，而mu[d]变成mu[T/p]也是很好理解的，注意这个p也是质数

所以这个式子的变形就是这样啦，然后感觉和BZOJ2301有点像了。

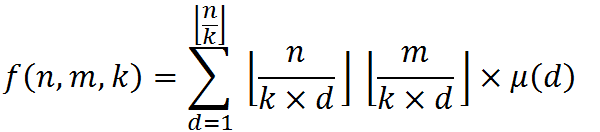[这是2301的图]

唯一区别就是一个是mu[]，一个是一大坨东西

于是我们设f(T)=sigma(p|T)mu[T/p]  可以看出这一堆只和T有关。

然后如果能预处理出来f(T)就可以了。

然后有种奥妙重重的做法，枚举每个素数然后去更新这些素数的倍数[然后好像就可以O(n)奥妙重重?因为蒟蒻不会算复杂度，但是这是可以A的]

然后当时宋老师提供了第二种思路，就是分析T的组成。

我们可以假设T=(p1^x1)*(p2^x2)*(p3^x3)...(pk^xk)

然后考虑若xi>=3 那么f(T)=0，因为不管怎么取，就算是除以pi，xi还是>=2的，所以mu[T/p]一定等于0，和也是0

若xi==2 && xj==2也有f(T)=0，理由同上

然后就只有两种情况了

xi==2 && 其他x等于1 ，这时只有取出pi时mu[T/pi]=(-1)^k，其他时候都是0

若 所有xi==1，取出来都等于(-1)^(k-1)，答案就是k*(-1)^(k-1)

然后据说你要是线性筛能得到每个数属于哪个范围就可以搞定这道题了。

当时听的时候觉得很兹瓷啊...但是发现我不能实现啊，于是就用唯一分解做了，然后好像最坏是n*log(n)的，然而过了...

所以怎么用线性筛呢...

[那就看聪明的读者您了...]

我的代码：

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int maxn=;

int Prime[maxn],cnt;
int f[maxn],nr[maxn],s[maxn];
bool np[maxn],zn[maxn];

inline int in(){
    int x=;char ch=getchar();
    while(ch>'' || ch<'') ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return x;
}

int get_f(int x){
    int k=,find=,rec;
    while(x>){
        if(rec==nr[x]){if(!find) find=true; else return ;}
        rec=nr[x],x/=nr[x],k++;
    }
    if(find){if(k&) return ; else return -;}
    else{if(k&) return k; else return -k;}
}

void get_prime(){
    for(int i=;i<maxn;i++){
        if(!np[i]){Prime[++cnt]=i;nr[i]=i;}
        for(int j=;j<=cnt && Prime[j]*i<maxn;j++){
            np[Prime[j]*i]=true,nr[Prime[j]*i]=Prime[j];
            if(i%Prime[j]==){
                zn[Prime[j]*i]=true;break;
            }
        }
    }
    for(int i=;i<maxn;i++) f[i]=get_f(i),s[i]=s[i-]+f[i];
}

long long calcu(int n,int m){
    long long sum=;
    if(n>m) swap(n,m);
    for(int i=,j=;i<=n;i=j+){
        j=min(n/(n/i),m/(m/i));
        sum+=(long long)(s[j]-s[i-])*(n/i)*(m/i);
    }
    return sum;
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("2820.in","r",stdin);
    freopen("2820.out","w",stdout);
#endif

    get_prime();

    int n,m,T=in();
    while(T--){
        n=in(),m=in();
        printf("%lld\n",calcu(n,m));
    }

    return ;
}