【27.48%】【codeforces 699D】 Fix a Tree

time limit per test2 seconds

memory limit per test256 megabytes

inputstandard input

outputstandard output

A tree is an undirected connected graph without cycles.

Let’s consider a rooted undirected tree with n vertices, numbered 1 through n. There are many ways to represent such a tree. One way is to create an array with n integers p1, p2, …, pn, where pi denotes a parent of vertex i (here, for convenience a root is considered its own parent).



For this rooted tree the array p is [2, 3, 3, 2].

Given a sequence p1, p2, …, pn, one is able to restore a tree:

There must be exactly one index r that pr = r. A vertex r is a root of the tree.

For all other n - 1 vertices i, there is an edge between vertex i and vertex pi.

A sequence p1, p2, …, pn is called valid if the described procedure generates some (any) rooted tree. For example, for n = 3 sequences (1,2,2), (2,3,1) and (2,1,3) are not valid.

You are given a sequence a1, a2, …, an, not necessarily valid. Your task is to change the minimum number of elements, in order to get a valid sequence. Print the minimum number of changes and an example of a valid sequence after that number of changes. If there are many valid sequences achievable in the minimum number of changes, print any of them.

Input

The first line of the input contains an integer n (2 ≤ n ≤ 200 000) — the number of vertices in the tree.

The second line contains n integers a1, a2, …, an (1 ≤ ai ≤ n).

Output

In the first line print the minimum number of elements to change, in order to get a valid sequence.

In the second line, print any valid sequence possible to get from (a1, a2, …, an) in the minimum number of changes. If there are many such sequences, any of them will be accepted.

Examples

input

4

2 3 3 4

output

1

2 3 4 4

input

5

3 2 2 5 3

output

0

3 2 2 5 3

input

8

2 3 5 4 1 6 6 7

output

2

2 3 7 8 1 6 6 7

Note

In the first sample, it’s enough to change one element. In the provided output, a sequence represents a tree rooted in a vertex 4 (because p4 = 4), which you can see on the left drawing below. One of other correct solutions would be a sequence 2 3 3 2, representing a tree rooted in vertex 3 (right drawing below). On both drawings, roots are painted red.

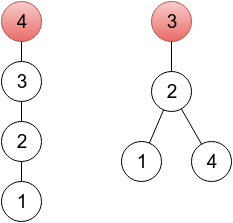
In the second sample, the given sequence is already valid.

【题解】



题意:

要把多个子图、可能带环的图合并成一颗树;只有n条边.

做法:

先确定树的根节点是什么;

如果一开始给的数据里面没有fa[i]==i的情况。

那么就在各个子图里面的环里面找一个根节点(因为没有fa[i]==i,则必然是所有的子图都存在环),随便找一个就可以了。

然后把各个子图的环中的任意一个节点改一下，接到根节点上就可以了;

链怎么办?如果是链那么肯定会有fa[i]==i这样的数据的；

比如2 3 4 4

最后的fa[4]==4,这样才是一条链。

那么我们访问到4的时候，再访问fa[4]就又为4了。则把fa[4]改成树的根节点(我们的程序会认为这是一个环).一切都顺理成章~~

提供两张图供理解

#include <cstdio>
#include <iostream>
#include <cstring>

using namespace std;

const int MAXN = 2e5 + 100;

int n, fa[MAXN],root = 0,vis[MAXN],cnt = 0,ans = 0;
bool rooted = false;

void input(int &r)
{
    r = 0;
    char t = getchar();
    while (!isdigit(t)) t = getchar();
    while (isdigit(t)) r = r * 10 + t - '0', t = getchar();
}

void dfs(int x)
{
    vis[x] = cnt;
    if (vis[fa[x]] == cnt) {//出现了环
        if (!rooted) {//如果之前还没找到一个根节点，那么这个节点作为根节点
            rooted = true;
            root = x;
        }
        fa[x] = root;
        ans++;
        return;
    }
    else
        if (vis[fa[x]] != -1)
            return;
    dfs(fa[x]);
}

int main()
{
    //freopen("F:\\rush.txt", "r", stdin);
    memset(vis, 255, sizeof(vis));
    input(n);
    for (int i = 1; i <= n; i++){
        input(fa[i]);
        if (fa[i] == i && !rooted){
            rooted = true;
            vis[i] = ++cnt;
            root = i;
        }
    }
    for (int i = 1; i <= n; i++)
        if (vis[i] == -1) {
            cnt++;
            dfs(i);
        }
    printf("%d\n", ans);
    for (int i = 1; i <= n; i++)
        printf("%d%c", fa[i], (i == n ?'\n':' '));
    return 0;
}