【bzoj2818】: Gcd 数论-欧拉函数

【bzoj2818】: Gcd

考虑素数p<=n

gcd(xp,yp)=p 当 gcd(x,y)=1 xp,yp<=n满足条件

p对答案的贡献：

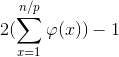
预处理前缀和就好了

 /* http://www.cnblogs.com/karl07/ */
 #include <cstdlib>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 using namespace std;

 #define ll long long
 const int N=1e7+;
 ll phi[N],prime[N];
 int cnt=,n;
 ll ans;

 void PHI(int n){
     phi[]=;
     for (int i=;i<=n;i++){
         if (!phi[i]){
             prime[++cnt]=i;
             for (int j=i;j<=n;j+=i){
                 if (phi[j]==) phi[j]=j;
                 phi[j]=phi[j]/i*(i-);
             }
         }
     }
 }

 int main(){
     scanf("%d",&n);
     PHI(n);
     for (int i=;i<=n;i++) phi[i]+=phi[i-];
     for (int i=;i<=cnt;i++){
         ans+=phi[n/prime[i]]*-;
     }
     printf("%lld\n",ans);
     return ;
 }