零零星星挖坑几个了，都没填土，实在是欠账太多，闲话少说吧，还是多记录总结一下。今天的主题是围绕convolution和加速

记得之前看过lecun他们组的一篇文章，是fft加速convolution的。按照Convolution Theorem，时域上的卷积可以转成空间域的傅立叶变换进行。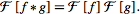

lecun的文章就是通过把卷积变成傅立叶变换实现加速的。从实验里看到，加速比2倍左右。目前这部分有代码开源，但是好像并没有merge到caffe中，原因可能是因为加速比例有限，再者消耗空间。猜测主要是加速比例问题吧，因为加速过程中，由于其原理，当卷积核小，是没什么加速的，当核是3或者5时，速度有的更慢或者相当，而在cnn中卷积的核大多数比较小，起到的加速作用很小，而基于图像处理本身目前的任务来说，卷积核一般不会太大，googlenet用7X7已经是爆炸天了。而从另外一方面来说，对caffe实现多GPU卡的加速或者多机的加速，则是实打实的加速，无论你的卷积核多大，你都能加速。

lecun他们又出了一篇新的文章，facebook的，Fast Convolutional Nets With fbfft: A GPU Performance Evaluation。caffe上已经有人实现了，加速1.4(3X3)到14.5倍。从他们的文章中看到，卷积核小的时候也是实现了加速了，赞。

待续……

convolution,fft, 加速的更多相关文章

  1. 51nod 算法马拉松 34 Problem D 区间求和2 （FFT加速卷积）

    题目链接  51nod 算法马拉松 34  Problem D 在这个题中$2$这个质数比较特殊,所以我们先特判$2$的情况,然后仅考虑大于等于$3$的奇数即可. 首先考虑任意一个点对$(i, j)$ ...

  2. P1919 FFT加速高精度乘法

    P1919 FFT加速高精度乘法 传送门:https://www.luogu.org/problemnew/show/P1919 题意: 给出两个n位10进制整数x和y,你需要计算x*y. 题解: 对 ...

  3. SPOJ - VFMUL - Very Fast Multiplication FFT加速高精度乘法

    SPOJ - VFMUL:https://vjudge.net/problem/SPOJ-VFMUL 这是一道FFT求高精度的模板题. 参考:https://www.cnblogs.com/Rabbi ...

  4. FFT初步学习小结

    FFT其实没什么需要特别了解的,了解下原理,(特别推荐算法导论上面的讲解),模板理解就行了.重在运用吧. 处理过程中要特别注意精度. 先上个练习的地址吧: http://vjudge.net/vjud ...

  5. FFT与多项式、生成函数题目泛做

    题目1 COGS 很强的乘法问题 高精度乘法用FFT加速 #include <cstdlib> #include <iostream> #include <algorit ...

  6. bzoj 3513: [MUTC2013]idiots FFT

    bzoj 3513: [MUTC2013]idiots FFT 链接 bzoj 思路 参考了学姐TRTTG的题解 统计合法方案,最后除以总方案. 合法方案要不好统计,统计不合法方案. \(a+b< ...

  7. 【XSY2166】Hope 分治 FFT

    题目描述 对于一个\(1\)到\(n\)的排列\(a_1,a_2,a_3,\ldots,a_n\),我们定义这个排列的\(P\)值和\(Q\)值: 对于每个\(a_i\),如果存在一个最小的\(j\) ...

  8. 【XSY2332】Randomized Binary Search Tree 概率DP FFT

    题目描述 \(\forall 0\leq i<n\),求有多少棵\(n\)个点,权值和优先级完全随机的treap的树高为\(i\). \(n\leq 30000\) 题解 设\(f_{i,j}\ ...

  9. 【BZOJ3771】Triple 生成函数 FFT 容斥原理

    题目大意 有\(n\)把斧头,不同斧头的价值都不同且都是\([0,m]\)的整数.你可以选\(1\)~\(3\)把斧头,总价值为这三把斧头的价值之和.请你对于每种可能的总价值,求出有多少种选择方案. ...

随机推荐

  1. Selenium2(WebDriver)中执行JavaScript代码 （转）

    在用selenium编写web页面的自动化测试代码时,可能需要执行一些JavaScript代码,selenium本身就支持执行js,我们在代码中可以使用executeScript.executeAsy ...

  2. Lights Out Game

    Lights Out Game 在线的游戏:http://www.neok12.com/games/lights-out/lights-out.htm 瞎试一阵子未成之后,终于找到了标准答案:http ...

  3. 性能测试工具LoadRunner27-LR之读取Excel数据

    为何要读取Excel数据? 很多用户喜欢用Excel来统计数据,比如学生成绩表.个人信息等.有时需要把Excel中的数据来进行参数化,数据量比较多时,一个个在LR里输入是不现实的,因此需要用LR来导入 ...

  4. jQuery源代码学习笔记_bind

    一般想到JS的兼容性问题的时候,首先会想到addEventListener与attachEvent这一对冤家,那么我们先来看看它们有什么兼容性问题 addEventListener与attachEve ...

  5. log4j.properties 日志分析

    # 多目的地.自定义样式#设置级别和多个目的地#level 是日志记录的优先级,分为 OFF.FATAL.ERROR.WARN.INFO.DEBUG.ALL或者您定义的级别.#Log4j建议只使用四个 ...

  6. php一种面向对象的语言，那么什么是面向对象呢？

    php一种面向对象的语言,那么什么是面向对象呢? 传统的面向过程的编程思想: 相信很多人第一次接触编程都是c语言,c语言就是非常典型的面向过程的编程语言,将要实现的功能描述为一个从开始到结束的连续的“ ...

  7. 【MATLAB】画信号频谱的子函数

    输入信号序列和采样率,该子函数可以画出该信号的频谱图. function [f,spec,NFFT]=spec_fft_plot(sample,L,Fs) % 输入数据说明: % sample:信号序 ...

  8. c\c++数据类型存储

    C四个 C++五个 一. 在c中分为这几个存储区 1.栈 - 由编译器自动分配释放 2.堆 - 一般由程序员分配释放,若程序员不释放,程序结束时可能由OS回收 3.全局区(静态区),全局变量和静态变量 ...

  9. 关于Authorware的十二种使用技巧

    Authorware是美国Macromedia公司(现已被adobe公司收购)开发的一种多媒体制作软件,它是一个图标导向式的多媒体开发工具.今天我们学习一下Authorware的十二种使用技巧,如果你 ...

  10. c++的bind1st()与bind2nd() 二元算子转一元算子

    bind1st()和bind2nd()是两个函数,用于将二元算子转成一元算子. 何谓二元算子? 比如< > =等等这些就是二元算子,即需要两个操作数的运算符. 何谓一元算子? 比如++ - ...