JS实现二叉树的创建和遍历

1、先说二叉树的遍历，遍历方式：

　　　前序遍历：先遍历根结点，然后左子树，再右子树

　　　中序遍历：先遍历左子树，然后根结点，再右子树

　　　后续遍历：先遍历左子树，然后右子树，再根结点

 

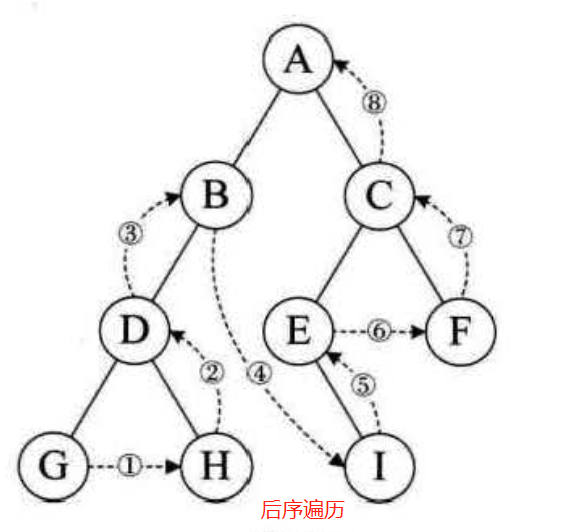
上代码：主要还是利用递归

function TreeCode() {
    let BiTree = function (ele) {
        this.data = ele;
        this.lChild = null;
        this.rChild = null;
    }
 
    this.createTree = function () {
        let biTree = new BiTree('A');
        biTree.lChild = new BiTree('B');
        biTree.rChild = new BiTree('C');
        biTree.lChild.lChild = new BiTree('D');
        biTree.lChild.lChild.lChild = new BiTree('G');
        biTree.lChild.lChild.rChild = new BiTree('H');
        biTree.rChild.lChild = new BiTree('E');
        biTree.rChild.rChild = new BiTree('F');
        biTree.rChild.lChild.rChild = new BiTree('I');
        return biTree;
    }
}
 
//前序遍历
function ProOrderTraverse(biTree) {
    if (biTree == null) return;
    console.log(biTree.data);
    ProOrderTraverse(biTree.lChild);
    ProOrderTraverse(biTree.rChild);
}
 
//中序遍历
function InOrderTraverse(biTree) {
    if (biTree == null) return;
    InOrderTraverse(biTree.lChild);
    console.log(biTree.data);
    InOrderTraverse(biTree.rChild);
}
 
//后续遍历
function PostOrderTraverse(biTree) {
    if (biTree == null) return;
    PostOrderTraverse(biTree.lChild);
    PostOrderTraverse(biTree.rChild);
    console.log(biTree.data);
}
 
let myTree = new TreeCode();
console.log(myTree.createTree());
console.log('前序遍历')
ProOrderTraverse(myTree.createTree());
console.log('中序遍历')
InOrderTraverse(myTree.createTree());
console.log('后续遍历')
PostOrderTraverse(myTree.createTree());

二叉树的非递归遍历

　　深度优先遍历（主要利用栈的先进后出）

　　广度优先遍历（主要利用队列的先进先出）

//深度优先非递归
function DepthFirstSearch(biTree) {
    let stack = [];
    stack.push(biTree);
 
    while (stack.length != 0) {
        let node = stack.pop();
        console.log(node.data);
        if (node.rChild) {
            stack.push(node.rChild);
        }
        if (node.lChild) {
            stack.push(node.lChild);
        }
 
    }
 
}
 
//广度优先非递归
function BreadthFirstSearch(biTree) {
    let queue = [];
    queue.push(biTree);
    while (queue.length != 0) {
        let node = queue.shift();
        console.log(node.data);
        if (node.lChild) {
            queue.push(node.lChild);
        }
        if (node.rChild) {
            queue.push(node.rChild);
        }
    }
 
}

深度优先主要是利用栈，先压右子树，再压左子树

广度优先主要利用队列，先入左子树，再入右子树

深度优先的遍历结果与前序遍历相同ABDGHCEIF，广度优先的遍历结果是 ABCDEFGHI

2、创建二叉树

　　1中创建二叉树的方式过于笨拙，假入我们根据完全二叉树的模型建立自己的二叉树，空数据的地方用#表示，如下图所示我们称之为扩展二叉树，我们取其前序遍历的序列 AB#D##C##。

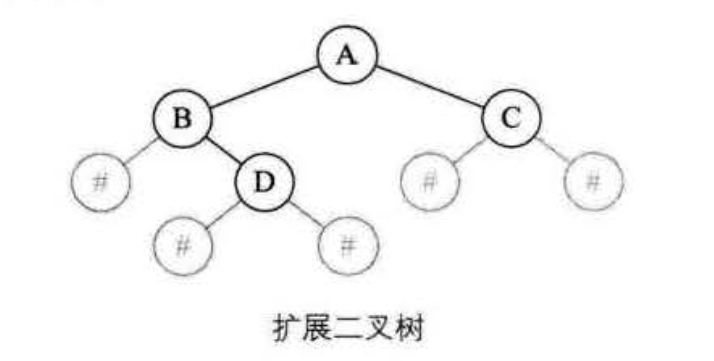
上代码：也是利用递归

//前序遍历得到的字符串
let strArr = 'AB#D##C##'.split('');
 
function BiTree(ele) {
    this.data = ele;
    this.lChild = null;
    this.rChild = null;
}
var newTree = new BiTree('#');
 
function createBiTree(biTree) {
    if (strArr.length == 0) return;
    let str = strArr.shift();
    if (str == '#') return;
    biTree.data = str;
    if (strArr[0] != '#') {
        biTree.lChild = new BiTree('#')
    }
    createBiTree(biTree.lChild);
    if (strArr[0] != '#') {
        biTree.rChild = new BiTree('#')
    }
    createBiTree(biTree.rChild);
}
createBiTree(newTree);
console.log(newTree);
ProOrderTraverse(newTree)

　　你也可以用中序遍历或者后序遍历实现二叉树的创建，代码里生成结点和构建左右子树的代码顺序交换一下就行了