2016 ICPC Mid-Central USA Region J. Windy Path (贪心)

比赛链接：2016 ICPC Mid-Central USA Region

题目链接：Windy Path

Description

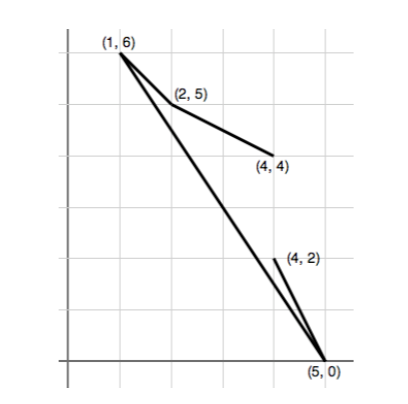
Consider following along the path in the figure above, starting from \((4,4)\) and moving to \((2,5)\). Then the path turns rightward toward \((1,6)\), then sharp left to \((5,0)\) and finally sharp left again to \((4,2)\). If we use ‘\(L\)’ for left and ‘RR’ for right, we see that the sequence of turn directions is given by RLL. Notice that the path does not cross itself: the only intersections of segments are the connection points along the path.

Consider the reverse problem: Given points in an arbitrary order,say \((2,5),(1,6),(4,4),(5,0),(4,2)\),could you find an ordering of the points so the turn directions along the path are given by RLL? Of course to follow the path in the figure,you would start with the third point in the list \((4,4)\),then the first \((2,5)\),second \((1,6)\), fourth \((5,0)\), and fifth \((4,2)\), so the permutation of the points relative to the given initial order would be: \(3\ 1 \ 2 \ 4 \ 5\).

Input

The first line of the input contains an integer \(N\), specifying the number of points such that \(3 \le N \le 50\). The following NN lines each describe a point using two integers \(x_i\) and \(y_i\) such that \(0 \le x_i,y_i \le 1000\). The points are distinct and no three are collinear (i.e., on the same line). The last line contains a string of \(N - 2\) characters, each of which is either ‘\(L\)’ or ‘\(R\)’.

Output

A permutation of\(\{ 1,...,N \}\) that corresponds to a nonintersecting path satisfying the turn conditions. The numbers are to be displayed with separating spaces. (There are always one or more possible solutions, and any one may be used.)

Solution

题意

给定 \(n\) 个点的坐标和一个包含 \(R\) 和 \(L\) 的序列，其中 \(L\) 代表左转，\(R\) 代表右转，求一个访问每个点顺序满足给定的序列。

题解

贪心 构造 计算几何

由于是 special judge，只要想出一种构造方法就可以。本题可以贪心。

1. 首先选择最下面最左边的点作为起点，(起点不唯一，比如最左边最下面也可以)。
2. 如果第一个字符是 \(R\)，第二个点选择最左边的点；反之选择最右边的点。
3. 之后每次考察连续两个字符：
   • 如果是 \(RL\)，选择右边最后一个
   • 如果是 \(LR\)，选择左边最后一个
   • 如果是 \(RR\)，选择右边第一个
   • 如果是 \(RR\)，选择左边第一个

判断点是在向量的左边还是右边可以用 \(ToLeftTest\)，查询第一个还是最后一个可以用夹角判断。

/*
    思路:
    贪心
    1. R: 左边第一个
    2. L: 右边第一个
    3. RL: 右边最后一个
    4. LR: 左边最后一个
    5. LL: 左边第一个
    6. RR: 右边第一个
 */

#include <bits/stdc++.h>
using namespace std;

struct Point {
    int x, y, index;
} p[100];

int area2(Point p, Point q, Point s) {
    return p.x * q.y - p.y * q.x + q.x * s.y - q.y * s.x + s.x * p.y - s.y * p.x;
}

// 判断某个点在向量的左边还是右边
bool toLeftTest(Point p, Point q, Point s) {
    return area2(p, q, s) > 0;
}

int cmp(Point p1, Point p2) {
    if (p1.y == p2.y)
        return p1.x < p2.x;
    return p1.y < p2.y;
}

// 求向量 pq 与 向量 ps 之间的夹角
double ang(Point p, Point q, Point s) {
    double x1 = q.x - p.x, y1 = q.y - p.y;
    double x2 = s.x - p.x, y2 = s.y - p.y;
    double ans = (x1 * x2 + y1 * y2) / (sqrt(x1 * x1 + y1 * y1) * sqrt(x2 * x2 + y2 * y2));
    return acos(ans);
}

vector<Point> ans; // 存放答案
int vis[100];      // 标记已访问过的点

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d%d", &p[i].x, &p[i].y);
        p[i].index = i;
    }
    sort(p + 1, p + n + 1, cmp);
    ans.push_back(p[1]); // 起点
    vis[p[1].index] = 1;
    double min_ang = 10;
    int min_index = 1;
    Point tmp, tmp2 = p[1]; // 保存上两个点

    string str;
    cin >> str;
    // 第一个点
    if (str[0] == 'R') {
        tmp.x = p[1].x - 1;
        tmp.y = p[1].y;
        for (int i = 2; i <= n; ++i) {
            double angle = ang(p[1], p[i], tmp);
            if (angle < min_ang) {
                min_ang = angle;
                min_index = i;
            }
        }
        ans.push_back(p[min_index]);
        vis[p[min_index].index] = 1;
    } else {
        tmp.x = p[1].x + 1;
        tmp.y = p[1].y;
        for (int i = 2; i <= n; ++i) {
            double angle = ang(p[1], p[i], tmp);
            if (angle < min_ang) {
                min_ang = angle;
                min_index = i;
            }
        }
        ans.push_back(p[min_index]);
        vis[p[min_index].index] = 1;
    }
    tmp = p[min_index];
    // 之后的点
    for (int i = 0; i < str.size() - 1; ++i) {
        if (str[i] == 'R' && str[i + 1] == 'L') {
            min_ang = 10;
            for (int i = 1; i <= n; ++i) {
                if (vis[p[i].index])
                    continue;
                if (toLeftTest(tmp2, tmp, p[i]))
                    continue;
                double angle = ang(tmp, tmp2, p[i]);
                if (min_ang > angle) {
                    min_ang = angle;
                    min_index = i;
                }
            }
            ans.push_back(p[min_index]);
            vis[p[min_index].index] = 1;
            tmp2 = tmp;
            tmp = p[min_index];
        }
        else if (str[i] == 'R' && str[i + 1] == 'R') {
            min_ang = 0;
            for (int i = 1; i <= n; ++i) {
                if (vis[p[i].index])
                    continue;
                if (toLeftTest(tmp2, tmp, p[i]))
                    continue;
                double angle = ang(tmp, tmp2, p[i]);
                if (min_ang < angle) {
                    min_ang = angle;
                    min_index = i;
                }
            }
            ans.push_back(p[min_index]);
            vis[p[min_index].index] = 1;
            tmp2 = tmp;
            tmp = p[min_index];
        } else if (str[i] == 'L' && str[i + 1] == 'R') {
            min_ang = 10;
            for (int i = 1; i <= n; ++i) {
                if (vis[p[i].index])
                    continue;
                if (!toLeftTest(tmp2, tmp, p[i]))
                    continue;
                double angle = ang(tmp, tmp2, p[i]);
                if (min_ang > angle)
                {
                    min_ang = angle;
                    min_index = i;
                }
            }
            ans.push_back(p[min_index]);
            vis[p[min_index].index] = 1;
            tmp2 = tmp;
            tmp = p[min_index];
        } else {
            min_ang = 0;
            for (int i = 1; i <= n; ++i) {
                if (vis[p[i].index])
                    continue;
                if (!toLeftTest(tmp2, tmp, p[i]))
                    continue;
                double angle = ang(tmp, tmp2, p[i]);
                if (min_ang < angle) {
                    min_ang = angle;
                    min_index = i;
                }
            }
            ans.push_back(p[min_index]);
            vis[p[min_index].index] = 1;
            tmp2 = tmp;
            tmp = p[min_index];
        }
    }
    // 最后一个点
    for (int i = 1; i <= n; ++i) {
        if (!vis[p[i].index]) {
            ans.push_back(p[i]);
            break;
        }
    }
    for (int i = 0; i < ans.size(); ++i) {
        printf("%d", ans[i].index);
        printf("%s", i == ans.size() - 1 ? "\n" : " ");
    }
    return 0;
}