Naive Bayes Algorithm And Laplace Smoothing

朴素贝叶斯算法(Naive Bayes)适用于在Training Set中，输入X和输出Y都是离散型的情况。如果输入X为连续，输出Y为离散，我们考虑使用逻辑回归(Logistic Regression)或者GDA(Gaussian Discriminant Algorithm)。

试想，当我们拿到一个全新的输入X,求解输出Y的分类问题时，相当于，我们要求解概率p(Y|X)这里的X和Y都是向量，我们要根据p(Y|X)的结果，找出可能性最大的那个y值，进行输出。举个经典的垃圾邮件(Spam)分类例子：如果在邮件中出现了"buy","discount","now"，但没有出现"sale","price"，试问这份邮件是垃圾邮件吗？首先我们将这5个单词分别对应到X中（顺序分别为"buy","discount","now","sale","price"）：

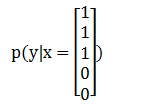
然后，我们要计算出p(y=1|x)和p(y=0|x)，以决定邮件是否为垃圾邮件。在实际情况中，X的维度可能是数万，甚至更多，直接求解的可能性为0，所以需要用到Naive Bayes。我们知道贝叶斯定理：

运用到此例子上，可以写为：

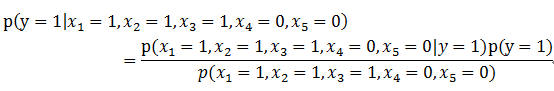
而Naive Bayes的Naive就在于，在给定y的情况下，我们认为X各个维度之间相互独立，即：

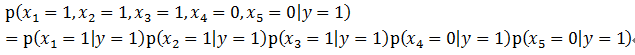所以有：

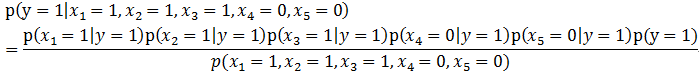
由全概率公式：

也就是说，我们预先通过建模，知道在一般情况下垃圾邮件的概率，以及垃圾邮件和非垃圾邮件中中，包含某一个词的概率，然后即可利用此公式进行计算。拓展到一般的情况：

拉普拉斯平滑，当在我们碰到没见过的xi，会导致上式的分子和分母都为0，则p(y=1|x)及p(y=0|x)的值无法得出，为了解决此问题，引入拉普拉斯平滑。下面先举例来说明：假设邮件分类中，有2个类，在指定的训练样本中，某个词语K1，观测计数分别为990，10，K1的概率为0.99，0.01，对这两个量使用拉普拉斯平滑的计算方法如下：991/1002=0.988，11/1002=0.012

通用版公式如下：

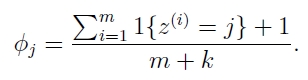
我最初的疑问是，为什么分母要加k(类别数)？因为你在k个分类概率的分子处都加了1，总共加了k个，为了保证全概率为1，所以分母也要加k。总体的思路是，异常值不要影响我们整体的概率。