poj 1179 Polygon

http://poj.org/problem?id=1179

Polygon

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5078		Accepted: 2139

Description

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N. 

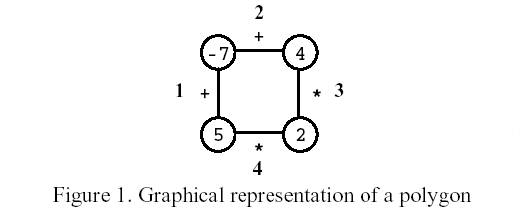
On the first move, one of the edges is removed. Subsequent moves involve the following steps: 
�pick an edge E and the two vertices V1 and V2 that are linked by E; and 
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2. 
The game ends when there are no more edges, and its score is the label of the single vertex remaining.

Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.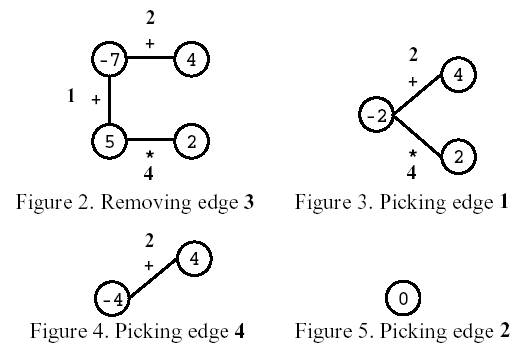 

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score. 

Input

Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices' labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *).

3 <= N <= 50 
For any sequence of moves, vertex labels are in the range [-32768,32767]. 

Output

Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

Source

IOI 1998

 

 

分析：

　　多边形游戏，有N个顶点的多边形，3 <= N <= 50 ，多边形有N条边，每个顶点中有一个数字（可正可负），每条边上或者是“+”号，或者是“*”号。边从1到N编号，首先选择一条边移去，然后进行如下操作：

1 选择一条边E和边E连接着的两个顶点V1，V2。

2 用一个新的顶点代替边E和V1、V2，新顶点的值为V1、V2中的值进行边上代表的操作得来（相加或相乘）

当最后只剩一个顶点，没有边时，游戏结束。现在的任务是编程求出最后的顶点能获得的最大值，以及输出取该最大值时，第一步需移去的边，如果有多条符合条件的边，按编号从小到大输出。

其实结题思路还是比较好想到的，枚举（枚举去掉的符号）+DP（记忆化搜索）就可以做到。但这里有一个BUG，就是负负得正，所以不能单一的枚举最大值，而要同时DP最小值。    

计算最大值：
   加法  max(i,j) = max(i,k)+max(k,j);
   乘法  max(i,j) = MAX(max（i,k）*max(k,j),max(i,k)*min(k,j),max(k,j)*min(i,k),min(i,k)*min(k,j));(i=<k<=j)

计算最小值：

   加法  min(i,j) = min(i,k)+min(k,j);
   乘法  min(i,j) = MIN(max（i,k）*max(k,j),min(i,k)*min(k,j),max(k,j)*min(i,k),min(i,k)*min(k,j));(i=<k<=j)

 

AC代码：

 

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <iostream>
 #include <stack>
 #include <set>
 #include <queue>
 #define MAX(a,b) (a) > (b)? (a):(b)
 #define MIN(a,b) (a) < (b)? (a):(b)
 #define mem(a) memset(a,0,sizeof(a))
 #define INF 1000000007
 #define MAXN 20005
 using namespace std;

 bool op[];
 int num[],dp_max[], dp_min[], n;
 bool vis_max[],vis_min[];
 int DP_MIN(int i,int j);
 int DP_MAX(int i,int j);

 int DP_MAX(int i,int j)//DP求区间最大值
 {
     int u = i*+j;
     if(vis_max[u])return dp_max[u];
     vis_max[u]=;
     if(j-i <= )
     {
         if(j==i)return dp_max[u]=num[i-];
         if(!op[i])return dp_max[u]=num[i-]+num[i];
         else return dp_max[u]=num[i-]*num[i];
     }
     dp_max[u] = -INF;
     for(int k=i;k<j;k++)
     {
         int l=DP_MIN(i,k);
         int r=DP_MIN(k+,j);
         int ll=DP_MAX(i,k);
         int rr=DP_MAX(k+,j);
         if(!op[k])dp_max[u] = MAX(dp_max[u], ll+rr);
         else dp_max[u] = MAX(dp_max[u], MAX(ll*rr,MAX(l*r,MAX(l*rr,r*ll))));
     }
     return dp_max[u];
 }

 int DP_MIN(int i,int j)//DP求区间最小值
 {
     int u = i*+j;
     if(vis_min[u])return dp_min[u];
     vis_min[u]=;
     if(j-i <= )
     {
         if(j==i)return dp_min[u]=num[i-];
         if(!op[i])return dp_min[u]=num[i-]+num[i];
         else return dp_min[u]=num[i-]*num[i];
     }
     dp_min[u] = INF;
     for(int k=i;k<j;k++)
     {
         int l=DP_MIN(i,k);
         int r=DP_MIN(k+,j);
         int ll=DP_MAX(i,k);
         int rr=DP_MAX(k+,j);
         if(!op[k])dp_min[u] = MIN(dp_min[u], l+r);
         else dp_min[u] = MIN(dp_min[u], MIN(ll*rr,MIN(l*r,MIN(l*rr,r*ll))));
     }
     return dp_min[u];
 }

 int main()
 {
     while(~scanf("%d%*c",&n))
     {
         mem(op);mem(dp_max);
         mem(num);mem(vis_min);
         mem(vis_max);
         int max=-INF,i;
         char ch;
         for(i=;i<n;i++)
         {
             scanf("%c %d%*c",&ch,&num[i]);
             op[i]=op[i+n]=(ch=='x');
             num[i+n]=num[i];
         }
         for(i=;i<n;i++)
         {
             max=MAX(max,DP_MAX(i+,i+n));
         }
         printf("%d\n",max);
         int ok=;
         for(i=;i<n;i++)
         {
             if(DP_MAX(i+,i+n) == max)
             {
                 if(ok){printf("%d",i+);ok=;}
                 else printf(" %d",i+);
             }
         }
         printf("\n");
     }
     return ;
 }

 #include<iostream>
 using namespace std;
 int v[]; //存放点中的数据,下标从1开始
 char op[]; //存放边,下标从1开始
 int max_score[][]; //max_score[i][j]表示从边i到边j所能取到的最大值
 int min_score[][]; //min_score[i][j]表示从边i到边j所能取到的最小值
 int n;  //边、点的数量 

 //计算最大最小值
 void calculate(int max_x, int min_x, char op, int max_y, int min_y, int &max, int &min)
 {
     if(op=='t')
     {
         max = max_x + max_y;
         min = min_x + min_y;
     }
     else  //乘法
     {
         int temp;
         max = min = max_x * max_y;

         temp = max_x * min_y;
         if(temp > max) max=temp;
         if(temp < min) min=temp;

         temp = min_x * max_y;
         if(temp > max) max=temp;
         if(temp < min) min=temp;

         temp = min_x * min_y;
         if(temp > max) max=temp;
         if(temp < min) min=temp;
     }
 }

 int getNum(int i) //处理可能的越界问题
 {
     if(i>n) i-=n;
     else if(i<) i += n;
     return i;
 }

 //使用动态规划找最大值并返回
 int dp()
 {
     int i,j,k,len, max_temp, min_temp, max_value, min_value, temp,ans;
     //初始化数组的边界值
     for(i=; i<=n; i++)
     {
         j=i-; //j代表i左边的边
         if(j==) j=n;

         if(op[i]=='t')
          max_score[i][i] = min_score[i][i] =  v[j] + v[i];
         else
          max_score[i][i] = min_score[i][i] =  v[j] * v[i];

         max_score[i][j] = min_score[i][j] = v[j];
     }

     ans=<<;
     for(len=; len<n; len++) //len代表从边i到边j包含多少条边
      for(i=; i<=n; i++) //i代表开始边
      {
             j=i+len-; //j代表结束边
             if(j>n) j-=n;
             //计算max[i][j] min[i][j]的值， max[i][j]=max{d[i][k-1] op[k] d[k+1][j]} i<=k<=j
             k=i;
             calculate(max_score[i][getNum(k-)], min_score[i][getNum(k-)], op[k], max_score[getNum(k+)][j], min_score[getNum(k+)][j], max_temp, min_temp);
             max_value=max_temp;
             min_value=min_temp;
             while(true)
             {
                 k++;
                 if(k>n) k-=n;
                 calculate(max_score[i][getNum(k-)], min_score[i][getNum(k-)], op[k], max_score[getNum(k+)][j], min_score[getNum(k+)][j], max_temp, min_temp);
                 if(max_temp > max_value) max_value=max_temp;
                 if(min_temp < min_value) min_value=min_temp;
                 if(k==j) break;
             }
             max_score[i][j]=max_value;
             min_score[i][j]=min_value;
             if(len==n- && max_value>ans) ans=max_value;
      }

      return ans;
 }

 int main()
 {
     int i,j,ans;
     bool first=true;;

     //读入数据
     cin>>n;
     for(i=; i<=n; i++)
     {
         cin>>op[i]>>v[i];
     }

     ans=dp();
     cout<<ans<<endl; //输出最大值
     //输出取最大值时，第一次移去的边
     for(i=; i<=n; i++)
     {
         j=i+n-;
         if(j>n) j -= n;

         if(max_score[i][j] == ans)
         {
             if(!first) cout<<" ";
             cout<<i-;
             first = false;
         }
     }
     if(max_score[][n-]==ans)
     {
          if(!first) cout<<" ";
          cout<<n;
     }
     cout<<endl;

     return ;
 }