牛顿插值法——用Python进行数值计算

　　拉格朗日插值法的最大毛病就是每次引入一个新的插值节点，基函数都要发生变化，这在一些实际生产环境中是不合适的，有时候会不断的有新的测量数据加入插值节点集，

因此，通过寻找n个插值节点构造的的插值函数与n+1个插值节点构造的插值函数之间的关系，形成了牛顿插值法。推演牛顿插值法的方式是归纳法，也就是计算Ln（x）- Ln+1（x），并且从n=1开始不断的迭代来计算n+1时的插值函数。

　　牛顿插值法的公式是：

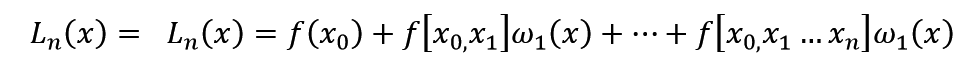
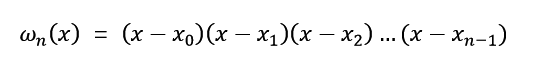
　　注意：在程序中我用W 代替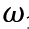 

　　计算牛顿插值函数关键是要计算差商，n阶差商的表示方式如下：

　　　　　　　　　　　　　　　　　　　　　　　　

　   关于差商我在这里并不讨论

　　计算n阶差商的公式是这样：

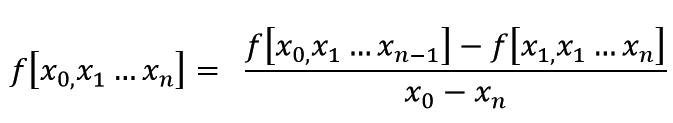
　　很明显计算n阶差商需要利用到两个n-1阶差商，这样在编程的时候很容易想到利用递归来实现计算n阶差商，不过需要注意的是递归有栈溢出的潜在危险，在计算差商的时候

更是如此，每一层递归都会包含两个递归，递归的总次数呈满二叉树分布：

　　　　

　　这意味着递归次数会急剧增加:(。所以在具体的应用中还需要根据应用来改变思路或者优化代码。

　　废话少说，放码过来。

　　首先写最关键的一步，也就是计算n阶差商：

"""
@brief:   计算n阶差商 f[x0, x1, x2 ... xn]
@param:   xi   所有插值节点的横坐标集合                                                        o
@param:   fi   所有插值节点的纵坐标集合                                                      /   \
@return:  返回xi的i阶差商(i为xi长度减1)                                                     o     o
@notice:  a. 必须确保xi与fi长度相等                                                        / \   / \
          b. 由于用到了递归，所以留意不要爆栈了.                                           o   o o   o
          c. 递归减递归(每层递归包含两个递归函数), 每层递归次数呈二次幂增长，总次数是一个满二叉树的所有节点数量(所以极易栈溢出)
"""
def get_order_diff_quot(xi = [], fi = []):
    if len(xi) > 2 and len(fi) > 2:
        return (get_order_diff_quot(xi[:len(xi) - 1], fi[:len(fi) - 1]) - get_order_diff_quot(xi[1:len(xi)], fi[1:len(fi)])) / float(xi[0] - xi[-1])
    return (fi[0] - fi[1]) / float(xi[0] - xi[1])

　　看上面的牛顿插值函数公式，有了差商，还差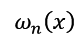

　　这个就比较好实现了：

"""
@brief:  获得Wi(x)函数;
         Wi的含义举例 W1 = (x - x0); W2 = (x - x0)(x - x1); W3 = (x - x0)(x - x1)(x - x2)
@param:  i  i阶(i次多项式)
@param:  xi  所有插值节点的横坐标集合
@return: 返回Wi(x)函数
"""
def get_Wi(i = 0, xi = []):
    def Wi(x):
        result = 1.0
        for each in range(i):
            result *= (x - xi[each])
        return result
    return Wi

　　　　

　　　　OK， 牛顿插值法最重要的两部分都有了，下面就是将这两部分组合成牛顿插值函数，如果是c之类的语言就需要保存一些中间数据了，我利用了Python的闭包直接返回一个牛顿插值函数，闭包可以利用到它所处的函数之中的上下文数据。

"""
@brief: 获得牛顿插值函数
@
"""
def get_Newton_inter(xi = [], fi = []):
    def Newton_inter(x):
        result = fi[0]
        for i in range(2, len(xi)):
            result += (get_order_diff_quot(xi[:i], fi[:i]) * get_Wi(i-1, xi)(x))
        return result
    return Newton_inter

　　　　上面这段代码就是对牛顿插值函数公式的翻译，注意get_Wi函数的参数是i-1，这个从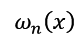函数的表达式可以找到原因。

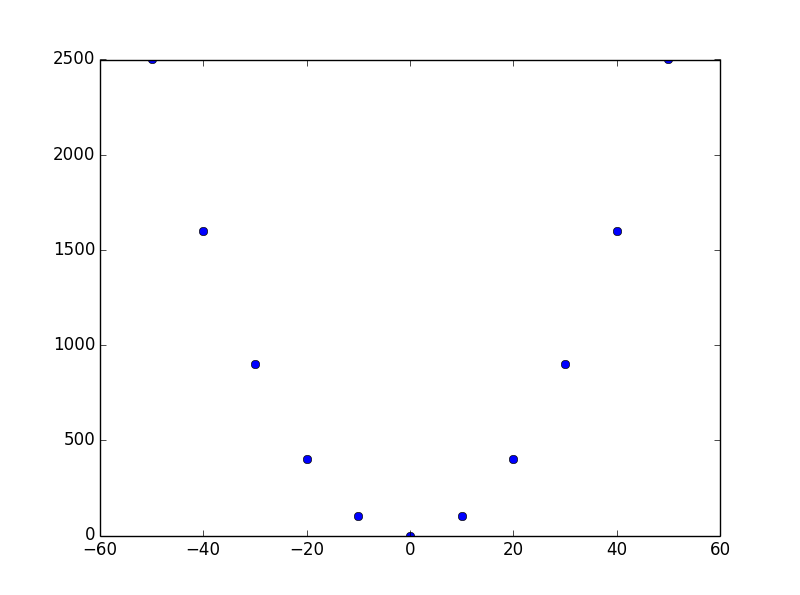
　　构造一些插值节点

　

 ''' 插值节点, 这里用二次函数生成插值节点，每两个节点x轴距离位10 '''
    sr_x = [i for i in range(-50, 51, 10)]
    sr_fx = [i**2 for i in sr_x]

　　　

　获得牛顿插值函数

    Nx = get_Newton_inter(sr_x, sr_fx)            # 获得插值函数

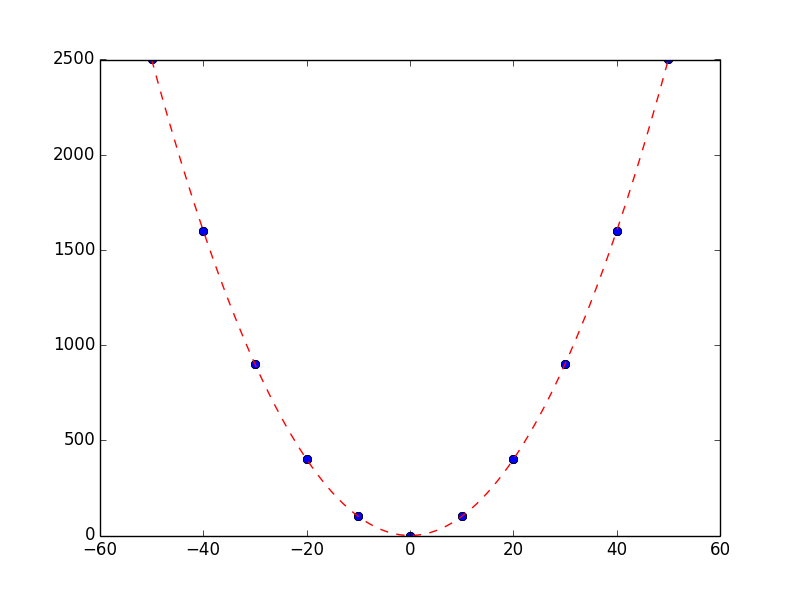
    tmp_x = [i for i in range(-50, 51)]          # 测试用例
    tmp_y = [Nx(i) for i in tmp_x]               # 根据插值函数获得测试用例的纵坐标

　　

完整代码：

# -*- coding: utf-8 -*-
"""
Created on Thu Nov 17 18:34:21 2016

@author: tete
@brief: 牛顿插值法
"""

import matplotlib.pyplot as plt

"""
@brief:   计算n阶差商 f[x0, x1, x2 ... xn]
@param:   xi   所有插值节点的横坐标集合                                                        o
@param:   fi   所有插值节点的纵坐标集合                                                      /   \
@return:  返回xi的i阶差商(i为xi长度减1)                                                     o     o
@notice:  a. 必须确保xi与fi长度相等                                                        / \   / \
          b. 由于用到了递归，所以留意不要爆栈了.                                           o   o o   o
          c. 递归减递归(每层递归包含两个递归函数), 每层递归次数呈二次幂增长，总次数是一个满二叉树的所有节点数量(所以极易栈溢出)
"""
def get_order_diff_quot(xi = [], fi = []):
    if len(xi) > 2 and len(fi) > 2:
        return (get_order_diff_quot(xi[:len(xi) - 1], fi[:len(fi) - 1]) - get_order_diff_quot(xi[1:len(xi)], fi[1:len(fi)])) / float(xi[0] - xi[-1])
    return (fi[0] - fi[1]) / float(xi[0] - xi[1])

"""
@brief:  获得Wi(x)函数;
         Wi的含义举例 W1 = (x - x0); W2 = (x - x0)(x - x1); W3 = (x - x0)(x - x1)(x - x2)
@param:  i  i阶(i次多项式)
@param:  xi  所有插值节点的横坐标集合
@return: 返回Wi(x)函数
"""
def get_Wi(i = 0, xi = []):
    def Wi(x):
        result = 1.0
        for each in range(i):
            result *= (x - xi[each])
        return result
    return Wi

"""
@brief: 获得牛顿插值函数
@
"""
def get_Newton_inter(xi = [], fi = []):
    def Newton_inter(x):
        result = fi[0]
        for i in range(2, len(xi)):
            result += (get_order_diff_quot(xi[:i], fi[:i]) * get_Wi(i-1, xi)(x))
        return result
    return Newton_inter

"""
demo:
"""
if __name__ == '__main__':   

    ''' 插值节点, 这里用二次函数生成插值节点，每两个节点x轴距离位10 '''
    sr_x = [i for i in range(-50, 51, 10)]
    sr_fx = [i**2 for i in sr_x]  

    Nx = get_Newton_inter(sr_x, sr_fx)            # 获得插值函数

    tmp_x = [i for i in range(-50, 51)]          # 测试用例
    tmp_y = [Nx(i) for i in tmp_x]               # 根据插值函数获得测试用例的纵坐标

    ''' 画图 '''
    plt.figure("I love china")
    ax1 = plt.subplot(111)
    plt.sca(ax1)
    plt.plot(sr_x, sr_fx, linestyle = '', marker='o', color='b')
    plt.plot(tmp_x, tmp_y, linestyle = '--', color='r')
    plt.show()