Hark的数据结构与算法练习之堆排序

前言

堆排序我是看了好半天别人的博客才有了理解，然后又费了九牛二虎之力才把代码写出来，我发现我的基础真的很差劲啊……不过自己选的路一定要坚持走下去。
我试着把我的理解描述出来，如有不妥之处希望大家可以指点出来

算法说明

堆排序，是基于堆的排序。 堆也就是二叉树的一种（完全二叉树），首先要确定堆的定义，才可以学会堆算法的逻辑；

OK，我们知道堆的定义前得先确定啥是完全二叉树。

二叉树就是树状结构是这样的，如图：

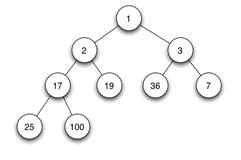
通常二叉树都会存放在数组中，那么将上图的完全二叉树放在数组中就是int[] arrayData = {1,2,3,17,19,36,7,25,100}

然后还有一个前置知识要知道，就是如何计算左子孩子的索引和右子孩子的索引。

还是以上图来举例子，3,36,7这三个数中， 3就是父节点，36 和 7就是子节点。  然后左子节点和右子节点的计算公式是i*2+1 和 i*2+2  。 替换到我举的例子中就是，数字3在数组中的索引是2，那么根据公式所述，左子节点的数组索引是2*2+1=5，右子节点的数组索引是2*2+2=6。 大家可以对一下数字36和数字7的数组索引和我们计算出来的是否一致。

还有，父节点的索引公式是 (i-1)/2。 大家可以代入一下上面的数组求一下值

OK，下面我们可以看一下堆的定义了。

堆的定义是这样的：

如图，堆分两种，一种是“小顶堆”，另一种是“大顶堆“。

小顶堆：就是顶点是最小值，并且父节点小于等于左子节点和右子节点（子节点公式上边有说）

大顶堆：就是顶点是最大值，并且父节点大于等于左子节点呼右子节点（子节点公式上边有说）

OK，现在说一下堆排序的逻辑。 堆排序是有两步：

第一步：建立堆。 我们需要把无序数组调整成堆结构（也就是让无序数组满足上图的条件）

大概过程，如图：

如图如所，我们要建立的是小顶堆，所以父节点一定是大小子节点的。

那么从97这个数字开始，是才有子节点的。  如果按公式来算，就是索引第(i/2)-1个数字是第一个有子节点的数字。

比较完数字97，把小的数字与97对换，然后再比较数字65与65子节点大小，然后再比较数字38与38子节点大小，最终比较最顶节点与子节点。

OK，有一个槽点要注意，请大家看第四图和第五图，当比较顶节点和子节点时，13与49换了位置，这时发现换位置后的49与49子节点是不满足堆的关联，所以49与27也要做一下互换的。   大家有个印象就行，具体逻辑还是请看下边的代码（17行至20行）

第二步：进行堆排序。

因为堆其实就是一个数组，所以如果我们的堆是完全从小到大，或者从大到小存储数据，那么数组同样也就是升序，或者降序了。

以下代码第24行至31行是进行堆排序。

我们可以看到我们之前代码建立好的堆是小顶堆，也就是最小值是在顶点。

第26行到28行，做的就是把第一个节点与最后一个节点数字互换，这时，最小值就在最后边了。

然后执行第30行的代码，因为上边把节点数字做了互换，这时堆就变成了无序数组，那么需要重新建立堆啦，需要把第一个节点至（最后一个节点-1）进行重建堆。

重建堆后，最小的数字又会放到第一他节点啦

接着执行第26行到28行，把第一个节点与（最后一个节点-1）数字互换，这时，最小值就在(最后一个节点-1)了。

然后执行第30行代码，继续重新建立堆。。。。如此类推，数字将会进行降序。

代码

使用JAVA

/*
 * 堆排序
 */
public class HeadSort {
	public static void main(String[] args) {
		int[] arrayData = { 5, 9, 6, 7, 4, 1, 2, 3, 8 };
		HeadSortMethod(arrayData);
		for (int integer : arrayData) {
			System.out.print(integer);
			System.out.print(" ");
		}
	}

	public static void HeadSortMethod(int[] arrayData) {
		// 第一步，将无序数组，建成一个堆。
		//System.out.println("开始建堆");
		for (int i = arrayData.length / 2 - 1; i >= 0; i--) {
			// 第一个有孩子节点的节点，索引是arrayData.length/2-1 。 这个就不证明了（暂时还不会），大家测试一下就知道结果了
			HeadAjust(arrayData, i, arrayData.length);
		}
		//System.out.println("开始排序");
		// 第二步，进行排序
		// 对堆进行递归，来建立排好序的堆。
		int temp;
		for (int i = arrayData.length-1; i > 0; i--) {
			temp = arrayData[0];
			arrayData[0] = arrayData[i];
			arrayData[i] = temp;

			HeadAjust(arrayData, 0, i - 1);
		}
	}

	/*
	 * 对于指定数组的序列，进行堆化调整 也就是将无序数组调整成堆。
	 */
	public static void HeadAjust(int[] arrayData, int beginIndex, int endIndex) {
		int minNum = arrayData[beginIndex];

		// i=beginIndex*2+1代表是左子节点
		// i=i*2+1代表下一个左子节点
		for (int i = beginIndex * 2 + 1; i <= endIndex; i = i * 2 + 1) {
			//System.out.println(i);
			// 先比较左子节点和右子节点， i存储小值的索引
			if (i < endIndex && arrayData[i] > arrayData[i + 1]) {
				i++;
			}

			if (arrayData[i] > minNum) {
				break;
			}

			arrayData[beginIndex] = arrayData[i];
			beginIndex = i;
		}

		arrayData[beginIndex] = minNum;
	}
}

执行结果：

9 8 7 6 5 4 3 2 1

　　

时间复杂度：O(nlog₂n)   参考这里http://blog.csdn.net/liliuteng/article/details/8496050， 说实在的，这个证明过程我还是看不太懂……数学基础不太好，过后需要再学习一下数学了。

空间复杂度：O(1)

学习资料

http://blog.csdn.net/clam_clam/article/details/6799763   本次总结大部分图是从这里来的…实在是懒着画了，抱歉抱歉

http://www.cnblogs.com/mengdd/archive/2012/11/30/2796845.html

http://blog.csdn.net/morewindows/article/details/6709644/