hihocoder 1196 高斯消元.二

传送门

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

在上一回中，小Hi和小Ho趁着便利店打折，买了一大堆零食。当他们结账后，看到便利店门口还有其他的活动。

店主：买了东西还可以参加游戏活动哦，如果能够完成游戏还有额外的奖品。

小Hi和小Ho赶紧凑了过去。

店主放了一块游戏板在店门口，有5行6列格子。左上角为坐标(1,1)。一部分格子是亮着的，另一部分是暗着的。

当按下某一个格子时，它和上下左右4个格子的状态就会改变。原来亮着的格子变成暗的，原来暗的格子会变亮。比如下图中按下标记有红叉的格子后，绿色虚线区域内的格子状态都会改变：

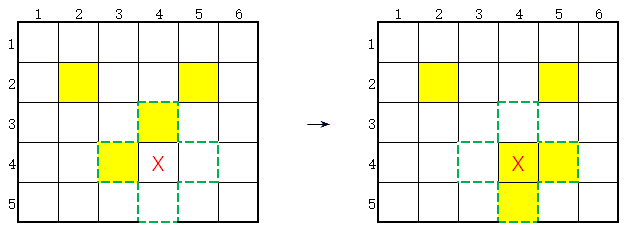
店主给出初始的状态，参加游戏的人员需要通过按下某些格子，让游戏板上所有的灯都亮起来就可以赢得奖品。

小Ho：这不就是开关灯问题么，看我来解决它！

本题改编自ACMICPC Greater New York 2002 EXTENDED LIGHTS OUT

提示：异或方程组

输入

第1..5行：1个长度为6的字符串，表示该行的格子状态，1表示该格子是亮着的，0表示该格子是暗的。

保证一定存在解，且一定存在暗着的格子。

输出

需要按下的格子数量k，表示按下这k个位置后就可以将整个游戏板所有的格子都点亮。

接下来k行，每行一个坐标(x,y)，表示需要按下格子(x,y)。x坐标较小的先输出，若x相同，则先输出y坐标较小的。

样例输入

001111
011111
111111
111110
111100

样例输出

2
1 1
5 6

---------------------------------------------------------------

异或方程组的形式为

a[0][0]*x[0] ^ a[0][1]*x[1] ^ ... ^ a[0][n-1]*x[n-1] = a[0][n]

a[1][0]*x[0] ^ a[1][1]*x[1] ^ ... ^ a[1][n-1]*x[n-1] = a[1][n]

　　　　　　　　　　　　　　　　　.

　　　　　　　　　　　　　　　　　.

a[n-1][0]*x[0] ^ a[n-1][1]*x[1] ^ ... ^ a[n-1][n-1]*x[n-1] = a[n-1][n]

方程组中所有量都是bool量

----------------------------------------------------------------

比较异或方程组和一般的线性方程组，不难发现：

除了所有加号（+）都换成了异或（^）外，形式上两者是完全一致的

因而对于异或方程组，我们考虑是否可用类似于高斯消元解线性方程组的方法来解。

这就是说我们希望通过行变换将系数矩阵转化成单位矩阵。

对此我们有下述结论可用：

----------------------------------------------------------------------------------------

若

a[0]*x[0] ^ a[1]*x[1] ^ ... ^ a[n-1]*x[n-1] = A

b[0]*x[0] ^ b[1]*x[1] ^ ... ^ b[n-1]*x[n-1] = B

则

(a[0]^b[0])*x[0] ^ (a[1]^b[1])*x[1] ^ ... ^ (a[n-1]^b[n-1])*x[n-1] = A ^ B

-----------------------------------------------------------------------------------------

实际上我们只要证明

a*x ^ b*x = (a ^ b)*x

上述结论便是很自然的推论了

而由于这里涉及的所有量都是bool值，只要枚举便能证明。

我们也可以从另一角度来看：

异或运算相当于模2下的加法运算，即

　　a ^ b = (a + b) % 2

我们有

(a*x + b*x) % 2

= ((a+b)*x) % 2

= ((a+b) % 2) * (x % 2) % 2

在 a, b, x都是bool量的情况下

上式即

a*x ^ b*x = (a ^ b)*x

这样异或（^）与加法（+）两种运算便自然联系起来了，异或方程组与一般的线性方程组本质上没有区别。

--------------------------------------------------------------------------------------------------------

异或方程组的高斯消元过程同样是：

枚举行，对第i行，在第i列选主元交换到第i行。将其余该列为1的行，用第i行与之异或。

--------------------------------------------------------------------------------------------------------

#include <bits/stdc++.h>
using namespace std;
char s[][];
int a[][];
int dx[]={, , , , -};
int dy[]={, , -, , };
int ok(int x, int y){
    return x>=&&x<&&y>=&&y<;
}
int swap(int i, int j){
    int tmp[];
    memcpy(tmp, a[i], sizeof(tmp));
    memcpy(a[i], a[j], sizeof(tmp));
    memcpy(a[j], tmp, sizeof(tmp));
}

int gauss(int n){
    for(int i=; i<n; i++){
        for(int j=i; j<n; j++)
            if(a[j][i]){
                swap(i, j);
                break;
            }
        for(int j=; j<n; j++)
            if(j!=i&&a[j][i]){
                //消去第j行第i项
                for(int k=i; k<=n; k++)
                    a[j][k]^=a[i][k];
            }
        //output();
    }
}

int main(){
    for(int i=; i<; i++)
        cin>>s[i];
    for(int i=; i<; i++)
        for(int j=; j<; j++){
            int now=*i+j;
            for(int k=; k<; k++){
                int x=i+dx[k], y=j+dy[k];
                if(ok(x, y)){
                    int nei=*x+y;
                    a[now][nei]=;
                }
            }
            a[now][]=(s[i][j]-'')^;
        }
    gauss();
    int ans=;
    for(int i=; i<; i++)
        ans+=a[i][];
    cout<<ans<<endl;
    for(int i=; i<; i++)
        if(a[i][])
            cout<<i/+<<' '<<i%+<<endl;
}