机器学习：线性判别式分析(LDA)

1.概述     

线性判别式分析（Linear Discriminant Analysis），简称为LDA。也称为Fisher线性判别（Fisher Linear Discriminant，FLD），是模式识别的经典算法，在1996年由Belhumeur引入模式识别和人工智能领域。

基本思想是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。

LDA与PCA都是常用的降维技术。PCA主要是从特征的协方差角度，去找到比较好的投影方式。LDA更多的是考虑了标注，即希望投影后不同类别之间数据点的距离更大，同一类别的数据点更紧凑。

但是LDA有两个假设:1.样本数据服从正态分布，2.各类得协方差相等。虽然这些在实际中不一定满足，但是LDA被证明是非常有效的降维方法，其线性模型对于噪音的鲁棒性效果比较好，不容易过拟合。

2.图解说明(图片来自网络)

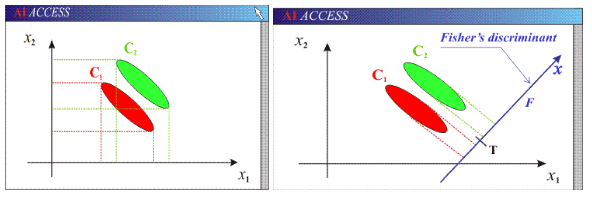
可以看到两个类别，一个绿色类别，一个红色类别。左图是两个类别的原始数据，现在要求将数据从二维降维到一维。直接投影到x1轴或者x2轴，不同类别之间会有重复，导致分类效果下降。右图映射到的直线就是用LDA方法计算得到的，可以看到，红色类别和绿色类别在映射之后之间的距离是最大的，而且每个类别内部点的离散程度是最小的（或者说聚集程度是最大的）。

3.图解LAD与PCA的区别(图片来自网络）

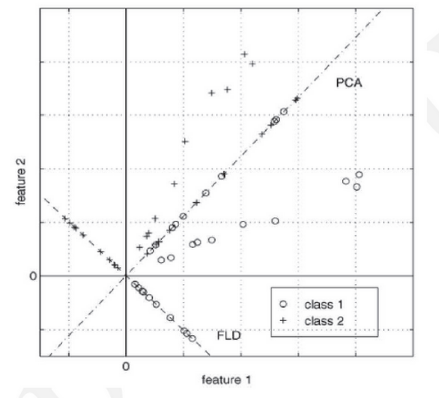
两个类别，class1的点都是圆圈，class2的点都是十字。图中有两条直线，斜率在1左右的这条直线是PCA选择的映射直线，斜率在 -1左右的这条直线是LDA选择的映射直线。其余不在这两条直线上的点是原始数据点。可以看到由于LDA考虑了“类别”这个信息（即标注），映射后，可以很好的将class1和class2的点区分开。

4.LAD与PCA的对比 

(1)PCA无需样本标签,属于无监督学习降维;LDA需要样本标签,属于有监督学习降维。二者均是寻找一定的特征向量w来降维的,其中LDA抓住样本的判别特征,PCA则侧重描叙特征。概括来说，PCA选择样本点投影具有最大方差的方向，LDA选择分类性能最好的方向。

     (2)PCA降维是直接和特征维度相关的,比如原始数据是d维的,那么PCA后可以任意选取1维、2维,一直到d维都行。LDA降维是直接和类别的个数C相关的,与数据本身的维度没关系,比如原始数据是d维的,一共有C个类别,那么LDA降维之后,一般就是1维,2维到C-1维进行选择。要求降维后特征向量维度大于C-1的,不能使用LDA。

(3）PCA投影的坐标系都是正交的,而LDA根据类别的标注关注分类能力,因此不保证投影到的坐标系是正交的（一般都不正交）

5.LAD的使用限制

(1)LDA至多可生成C-1维子空间
          LDA降维后的维度区间在[1,C-1]，与原始特征数n无关，对于二值分类，最多投影到1维。

(2)LDA不适合对非高斯分布样本进行降维。如下图所示的数据分布分类效果不好

（3）LDA在样本分类信息依赖方差而不是均值时，效果不好。

6.实验及讲解

1）生成实验数据，如下图：

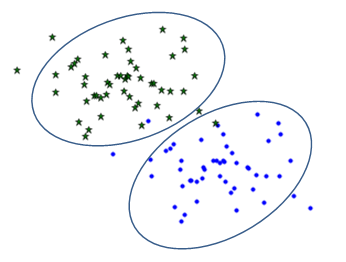
寻找一条直线，使按照椭圆圈出的分类进行投影，使得投影后模式样本在新的子空间有最大的类间距离和最小的类内距离。

2）核心函数

a）sklearn.discriminant_analysis.LinearDiscriminantAnalysis

b）主要参数(详细参数)

n_components ：减少到多少维空间

c）主要属性

coef_ ：权重。如果是投影到一维空间，则两个值对应的是直线的斜率和截距。

classes_ ：分类

3）详细代码

from sklearn.datasets.samples_generator import make_blobs
import numpy as np
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from itertools import cycle

##产生随机数据的中心
centers = [[2.5, 2],[1.8, 3] ]
##产生的数据个数
n_samples=100
##生产数据
X, labels = make_blobs(n_samples=n_samples, centers= centers, cluster_std=0.3,
                  random_state =0)

clf = LinearDiscriminantAnalysis()
clf.fit(X,labels)

##直线的斜率和截距
#print(clf.coef_) #-7.16451571  10.65392594]

##选取两个数进行预测
#print(clf.predict([[1.8, 3.2]]))  #1
#print(clf.predict([[2.7, 1.7]]))#0

##读取直线的斜率和截距
k1 = clf.coef_[0,0]
b1 = clf.coef_[0,1]

##绘图
plt.figure(1)
plt.clf()

'''
    说明：
     1）为了方便计算及说明，函数式1、2都采用了近似值
        y的斜率为-7.165，所以y1的斜率为0.14
     2）由于近似值或者绘图精度的问题，当y1斜率为0.14时与y不垂直，
        效果图中的绿色直线是下面函数绘制的：y1=0.37*x+1.7，即斜率为0.37
'''
#画LDA直线
x=np.linspace(0,4,50) ##在0-15直接画100个连续点
#y=k1*x+b1
y=-7.165*x+10.7 ##函数式1
plt.plot(x,y,color="red",linewidth=2)
#画与LDA直线垂直的直线
y1=0.14*x+2.2 ##函数式2
#y1=0.37*x+1.7  ##这个函数仅仅是为了绘制效果图用
plt.plot(x,y1,color="g",linewidth=2)

colors = cycle('mykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(len(clf.classes_)), colors):
    ##根据lables中的值是否等于k，重新组成一个True、False的数组
    my_members = labels == k
    ##X[my_members, 0] 取出my_members对应位置为True的值的横坐标
    plt.plot(X[my_members, 0], X[my_members, 1],'o',c = col ,markersize=4)

plt.axis([0, 4, 0, 5])
plt.show()

4）结果图

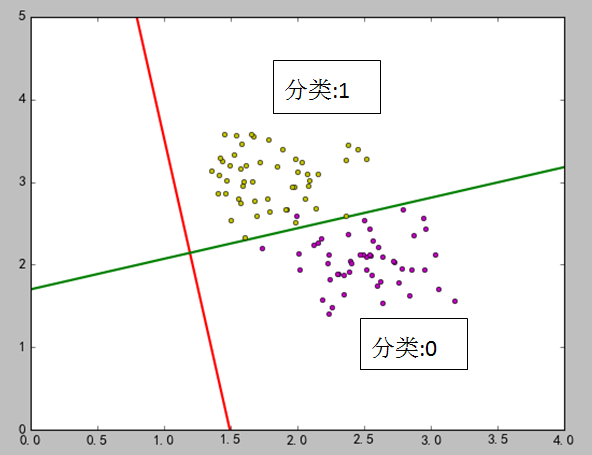
在上图中，红线是LDA之后求出来的，绿线是通过数学的两直线相交的关系求出来的。在代码中，选取了两个点：[1.8, 3.2]，[2.7, 1.7]，如果直接用训练出的模型进行预测，点[1.8, 3.2] 属于类型1，点[2.7, 1.7]属于类型0.如果通过线与点的关系，使用绿线进行判断，0.14×1.8+2.2=2.45 <3.2,所以点[1.8, 3.2]在绿线上面，因此属于分类1。0.14×2.7+2.2=2.578>1.7，所以点[2.7, 1.7]在绿线下面，因此属于分类0.

对应投影是一维的情况，个人感觉如果能求出绿线的方程，无论是从预测计算还是理解，都比较方便。但是由于样本点分布的不确定性，绿线的斜率好求，但是截距难找，所以LDA算法并没有给出相关的属性内容。