python实现折半查找算法&&归并排序算法

今天依旧是学算法，前几天在搞bbs项目，界面也很丑，评论功能好像也有BUG。现在不搞了，得学下算法和数据结构，笔试过不了，连面试的机会都没有……

今天学了折半查找算法，折半查找是蛮简单的，但是归并排序我就挺懵比，看教材C语言写的归并排序看不懂，后来参考了别人的博客，终于搞懂了。

折半查找

先看下课本对于 折半查找的讲解。注意了，折半查找是对于有序序列而言的。每次折半，则查找区间大约缩小一半。low,high分别为查找区间的第一个下标与最后一个下标。出现low>high时，说明目标关键字在整个有序序列中不存在，查找失败。

看我用python编程实现:

 def BinSearch(array, key, low, high):
     mid = int((low+high)/2)
     if key == array[mid]:  # 若找到
         return array[mid]
     if low > high:
         return False

     if key < array[mid]:
         return BinSearch(array, key, low, mid-1)  #递归
     if key > array[mid]:
         return BinSearch(array, key, mid+1, high)

 if __name__ == "__main__":
     array = [4, 13, 27, 38, 49, 49, 55, 65, 76, 97]
     ret = BinSearch(array, 76, 0, len(array)-1)  # 通过折半查找，找到65
     print(ret)

输出: 在列表中查找76.

76

时间复杂度：O(logn)

归并排序算法

先阐述一下排序思路：

首先归并排序使用了二分法，归根到底的思想还是分而治之。归并排序是指把无序的待排序序列分解成若干个有序子序列，并把有序子序列合并为整体有序序列的过程。长度为1的序列是有序的。因此当分解得到的子序列长度大于1时，应继续分解，直到长度为1.

(下图是分解过程，图自http://www.cnblogs.com/piperck/p/6030122.html)

合并的过程如下:

很好，你现在可以和别人说，老子会归并排序了。但是让你写代码出来，相信你是不会的……

来来来，看我用python写的归并排序算法:

 def merge_sort(array):  # 递归分解
     mid = int((len(array)+1)/2)
     if len(array) == 1:  # 递归结束的条件，分解到列表只有一个数据时结束
         return array
     list_left = merge_sort(array[:mid])
     list_right = merge_sort(array[mid:])
     print(">>>list_left:", list_left)
     print(">>>list_right:", list_right)
     return merge(list_left, list_right)  # 进行归并

 def merge(list_left, list_right):  # 进行归并
     final = []
     while list_left and list_right:
         if list_left[0] <= list_right[0]:  # 如果将"<="改为"<",则归并排序不稳定
             final.append(list_left.pop(0))
         else:
             final.append(list_right.pop(0))

     return final+list_left+list_right  # 返回排序好的列表

 if __name__=="__main__":
     array = [49, 38, 65, 97, 76]
     print(merge_sort(array))

输出:

>>>list_left: [49]
>>>list_right: [38]
>>>list_left: [38, 49]
>>>list_right: [65]
>>>list_left: [97]
>>>list_right: [76]
>>>list_left: [38, 49, 65]
>>>list_right: [76, 97]
[38, 49, 65, 76, 97]

时间度杂度: 平均情况＝最好情况＝最坏情况＝O(nlogn)

空间复杂度: O(n)

稳定性: 稳定

对序列{ 6, 5, 3, 1, 8, 7, 2, 4 }进行归并排序的实例如下:

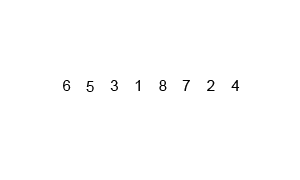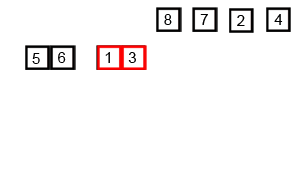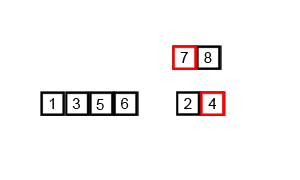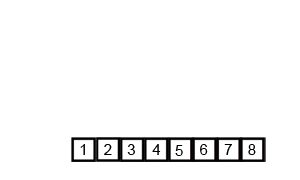
使用归并排序为一列数字进行排序的宏观过程: