「Codeforces 724F」Uniformly Branched Trees

题目大意

如果两棵树可以通过重标号后变为完全相同，那么它们就是同构的。

将中间节点定义为度数大于 \(1\) 的节点。计算由 \(n\) 个节点，其中所有的中间节点度数都为 \(d\) 的互不同构的树的数量。

答案对大质数取模。\(1\leq n\leq 1000,2\leq d \leq 10,10^{8}\leq \text{mod} \leq 10^9\)。

Solution

Part 1

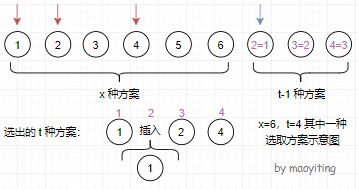
先来思考一个组合问题：在 \(x\) 个方案中不分顺序地选 \(t\) 种，可重复。求方案数。

这里给出一种非插板法的组合意义的解释：问题在于如何处理“可重复”这个条件。考虑在 \(x\) 种方案后面额外添加进去 \(t-1\) 种方案。前面 \(x\) 种方案中的第 \(i\) 种方案，表示选择了第 \(i\) 种方案。后面的 \(t-1\) 种方案中的第 \(i\) 种方案，表示 选出的 第 \(i+1\) 种方案与第 \(i\) 种一样。可以发现，在这 \(x+t-1\) 种方案中任选 \(t\) 个的方案数就是答案。所以方案数为 \(\dbinom{x+t-1}{t}\)。

Part 2

然后再来看这道题。

如何判断两棵无根树是否同构呢？由于无根树是可以重标号（换根）的，所以我们需要对于每棵无根树找出一个特殊的根，将无根树转化为有根树，才能方便比较同构。

对于无根树而言，能够确定的一个点就是 重心。重心有一个特殊的性质：一棵具有 \(n\) 个节点的无根树，若以该树的重心作为整棵树的根，则任意子树大小都小于 \(\frac{n}{2}\)。有两种情况：单重心 与 双重心。

令 \(dp_{i,j,k}\) 表示节点数为 \(i\)，有 \(j\) 棵子树，子树大小都不超过 \(k\) 的有根树数量。

有两种情况：

• 所有子树大小都不超过 \(k\)：\(dp_{i,j,k}←dp_{i,j,k-1}\)。

• 不满足“所有子树大小都不超过 \(k\)”：不满足“所有子树大小都不超过 \(k\)”意味着至少有一棵子树的大小是 \(k\)。考虑枚举子树大小等于 \(k\) 的子树个数。假设有 \(t\) 棵子树大小等于 \(k\)。由于子树之间是可以相同的（即 可重复），所以这 \(t\) 棵子树的方案数就是从 \(dp_{k,d-1,k-1}\) （\(d\) 就是题目中的 \(d\)）种方案中不分顺序地选 \(t\) 种并且可重复的方案数。实际上就是我们最开始思考的那个组合问题。所以方案数为 \(\dbinom{dp_{k,d-1,k-1}+t-1}{t}\)。则 \(dp_{i,j,k}←dp_{i-t\times k,j-t,k-1}\times \dbinom{dp_{k,d-1,k-1}+t-1}{t}\)。

若只考虑单重心，那么答案为 \(dp_{n,d,\lfloor \frac{n}{2}\rfloor}\)。

Part 3

然后考虑双重心的情况。出现了双重心，那么肯定是一条边连接的两个点分别挂着两棵大小相等的子树。大概长这样：

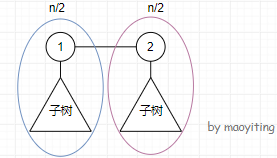
显然只有 \(n\) 是 偶数 时才会出现双重心。如图所示，把整棵树拆成两部分，就转化成了两个单重心。对于其中一部分的方案数为 \(dp_{\frac{n}{2},d-1,\lfloor \frac{n}{2}\rfloor -1}\)。所以双重心的情况的个数为，从 \(dp_{\frac{n}{2},d-1,\lfloor \frac{n}{2}\rfloor -1}\) 种方案中选出 \(2\) 种的方案数，则方案数为 \(\dbinom{dp_{\frac{n}{2},d-1,\lfloor \frac{n}{2}\rfloor -1}}{2}\)。

Part 4

综上所述：

• 当 \(n\) 是奇数时，答案为 \(dp_{n,d,\lfloor \frac{n}{2}\rfloor}\)。
• 当 \(n\) 是偶数时，答案为 \(dp_{n,d,\lfloor \frac{n}{2}\rfloor}-\dbinom{dp_{\frac{n}{2},d-1,\lfloor \frac{n}{2}\rfloor -1}}{2}\)。（为什么是单重心的情况个数减双重心的情况个数呢？因为每个双重心的情况都在前面算单重心的情况中算了两遍，一遍是以其中一个重心为根，一遍是以另一个重心为根。所以去掉重复的部分就是答案。）

Code

注意到要求的组合数 \(\binom{n}{m}\)，\(n\) 都比较大，\(m\) 都比较小。

\(C_n^m=\frac{n!}{m!(n-m)!}\) ，因为 \(m\) 非常小，所以 \(m!\) 可以很快被计算出来。

再考虑 \(\frac{n!}{(n-m)!}\)。\(\frac{n!}{(n-m)!}=\frac{n\times (n-1)\times ...\times (n-m+1)\times (n-m)\times (n-m-1)\times ...\times 2\times 1}{(n-m)\times (n-m-1)\times ...\times 2\times 1}=n\times (n-1)\times ...\times (n-m+1)\)。只有 \(m\) 项。也可以暴力计算。

代码里是预处理出 \(\frac{1}{i!}\)，然后用这样的方法计算。

另外 \(n\leq 2\) 的时候要特判，dp 边界条件也要注意。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e3+5,M=20;
int n,d,mod,dp[N][M][N],f[M],g[M],ans;
int mul(int x,int n,int mod){
    int ans=mod!=1;
    for(x%=mod;n;n>>=1,x=x*x%mod)
        if(n&1) ans=ans*x%mod;
    return ans;
}
void init(){
    int n=10;
    f[0]=g[0]=1;
    for(int i=1;i<=n;i++)
        f[i]=f[i-1]*i%mod;
    g[n]=mul(f[n],mod-2,mod);
    for(int i=n-1;i;i--)
        g[i]=g[i+1]*(i+1)%mod;    //计算 1/(i!)
}
int C(int n,int m){    //计算组合数
    if(n<m) return 0;
    int ans=1;
    for(int i=1;i<=m;i++)
        ans=ans*(n-i+1)%mod;
    return ans*g[m]%mod;
}
signed main(){
    scanf("%lld%lld%lld",&n,&d,&mod),init();
    if(n<=2) puts("1"),exit(0);    //特判
    for(int i=0;i<=n;i++) dp[1][0][i]=1;
    for(int i=2;i<=n;i++)    //枚举节点数
        for(int j=1;j<=min(i-1,d);j++)    //枚举子树个数
            for(int k=1;k<=n;k++){    //枚举子树大小的限制
                dp[i][j][k]=dp[i][j][k-1];    //所有子树大小都不超过 k 的情况
                for(int t=1;i-t*k>0&&j-t>=0;t++){    //t 棵子树大小等于 k
                    if(k!=1) dp[i][j][k]=(dp[i][j][k]+dp[i-t*k][j-t][k-1]*C(dp[k][d-1][k-1]+t-1,t)%mod)%mod;
                    else dp[i][j][k]=(dp[i][j][k]+dp[i-t*k][j-t][k-1]*C(dp[k][0][k-1]+t-1,t)%mod)%mod;
                }
            }
    if(n&1) ans=dp[n][d][n/2];    //n 为奇数
    else ans=(dp[n][d][n/2]-C(dp[n/2][d-1][n/2-1],2)+mod)%mod;    //n 为偶数
    printf("%lld\n",ans);
    return 0;
}