点到圆弧的距离(csu1503)+几何

1503: 点到圆弧的距离

Time Limit: 1 Sec  Memory Limit: 128 MB  Special Judge
Submit: 325  Solved: 70
[Submit][Status][Web
Board]

Description

输入一个点P和一条圆弧（圆周的一部分），你的任务是计算P到圆弧的最短距离。换句话说，你需要在圆弧上找一个点，到P点的距离最小。
提示：请尽量使用精确算法。相比之下，近似算法更难通过本题的数据。

Input

输入包含最多10000组数据。每组数据包含8个整数x1,
y1, x2, y2, x3, y3, xp, yp。圆弧的起点是A(x1,y1)，经过点B(x2,y2)，结束位置是C(x3,y3)。点P的位置是
(xp,yp)。输入保证A, B, C各不相同且不会共线。上述所有点的坐标绝对值不超过20。

Output

对于每组数据，输出测试点编号和P到圆弧的距离，保留三位小数。你的输出和标准输出之间最多能有0.001的误差。

Sample Input

0 0 1 1 2 0 1 -1
3 4 0 5 -3 4 0 1

Sample Output

Case 1: 1.414
Case 2: 4.000

HINT

 

Source

湖南省第十届大学生计算机程序设计竞赛

 

思路：根据三点确定圆心和半径；关键是确定扇形区域（尤其是优弧）

 

 

 

 

确定点在扇形区域就分两种情况，在圆内和圆外；不在扇形区域就是min(到A，到C)距离最短的；

 

 

转载请注明出处：寻找&星空の孩子 

 

题目链接：http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1503#userconsent#

 

具体见代码：

 

 #include<stdio.h>
 #include<math.h>
 #define PI acos(-1.0)
 #include<algorithm>
 using namespace std;
 struct Point
 {
     double x;
     double y;
     Point(double x=,double y=):x(x),y(y) {} //构造函数，方便代码编写
 } pt;
 struct Traingle
 {
     struct Point p[];
 } Tr;
 struct Circle
 {
     struct Point center;
     double r;
 } ans;
 //计算两点距离
 double Dis(struct Point p, struct Point q)
 {
     double dx=p.x-q.x;
     double dy=p.y-q.y;
     return sqrt(dx*dx+dy*dy);
 }
 //计算三角形面积
 double Area(struct Traingle ct)
 {
     return fabs((ct.p[].x-ct.p[].x)*(ct.p[].y-ct.p[].y)-(ct.p[].x-ct.p[].x)*(ct.p[].y-ct.p[].y))/2.0;
 }
 //求三角形的外接圆，返回圆心和半径(存在结构体"圆"中)
 struct Circle CircumCircle(struct Traingle t)
 {
     struct Circle tmp;
     double a, b, c, c1, c2;
     double xA, yA, xB, yB, xC, yC;
     a = Dis(t.p[], t.p[]);
     b = Dis(t.p[], t.p[]);
     c = Dis(t.p[], t.p[]);
 //根据 S = a * b * c / R / 4;求半径 R
     tmp.r = (a*b*c)/(Area(t)*4.0);
     xA = t.p[].x;
     yA = t.p[].y;
     xB = t.p[].x;
     yB = t.p[].y;
     xC = t.p[].x;
     yC = t.p[].y;
     c1 = (xA*xA+yA*yA - xB*xB-yB*yB) / ;
     c2 = (xA*xA+yA*yA - xC*xC-yC*yC) / ;
     tmp.center.x = (c1*(yA - yC)-c2*(yA - yB)) / ((xA - xB)*(yA - yC)-(xA - xC)*(yA - yB));
     tmp.center.y = (c1*(xA - xC)-c2*(xA - xB)) / ((yA - yB)*(xA - xC)-(yA - yC)*(xA - xB));
     return tmp;
 }

 typedef Point Vector;

 Vector operator + (Vector A,Vector B)
 {
     return Vector(A.x+B.x,A.y+B.y);
 }

 Vector operator - (Point A,Point B)
 {
     return Vector(A.x-B.x,A.y-B.y);
 }

 Vector operator * (Vector A,double p)
 {
     return Vector(A.x*p,A.y*p);
 }

 Vector operator / (Vector A,double p)
 {
     return Vector(A.x/p,A.y/p);
 }

 bool operator < (const Point& a,const Point& b)
 {
     return a.x<b.x||(a.x==b.x && a.y<b.y);
 }

 const double eps = 1e-;

 int dcmp(double x)
 {
     if(fabs(x)<eps)return ;
     else return x <  ? - : ;
 }
 bool operator == (const Point& a,const Point& b)
 {
     return dcmp(a.x-b.x)== && dcmp(a.y-b.y)==;
 }

 double Dot(Vector A,Vector B)
 {
     return A.x*B.x+A.y*B.y;
 }
 double length(Vector A)
 {
     return sqrt(Dot(A,A));
 }
 double Angle(Vector A,Vector B)
 {
     return acos(Dot(A,B)/length(A)/length(B));
 }

 double Cross(Vector A,Vector B)
 {
     return A.x*B.y-B.x*A.y;
 }
 double Area2(Point A,Point B,Point C)
 {
     return Cross(B-A,C-A);
 }
 double len;

 int main()
 {
     int ca=;
     while(scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&Tr.p[].x,&Tr.p[].y,&Tr.p[].x,&Tr.p[].y,&Tr.p[].x,&Tr.p[].y,&pt.x,&pt.y)!=EOF)
     {
         //      printf("%lf %lf\n%lf %lf\n%lf %lf\n%lf %lf\n",Tr.p[0].x,Tr.p[0].y,Tr.p[1].x,Tr.p[1].y,Tr.p[2].x,Tr.p[2].y,pt.x,pt.y);
         Circle CC=CircumCircle(Tr);
         //      printf("%lf %lf,r=%lf",CC.center.x,CC.center.y,CC.r);
         Point A(Tr.p[].x,Tr.p[].y),O(CC.center.x,CC.center.y),C(Tr.p[].x,Tr.p[].y),D(pt.x,pt.y),B(Tr.p[].x,Tr.p[].y);

         Vector OA(A-O),OB(B-O),OC(C-O),OD(D-O);
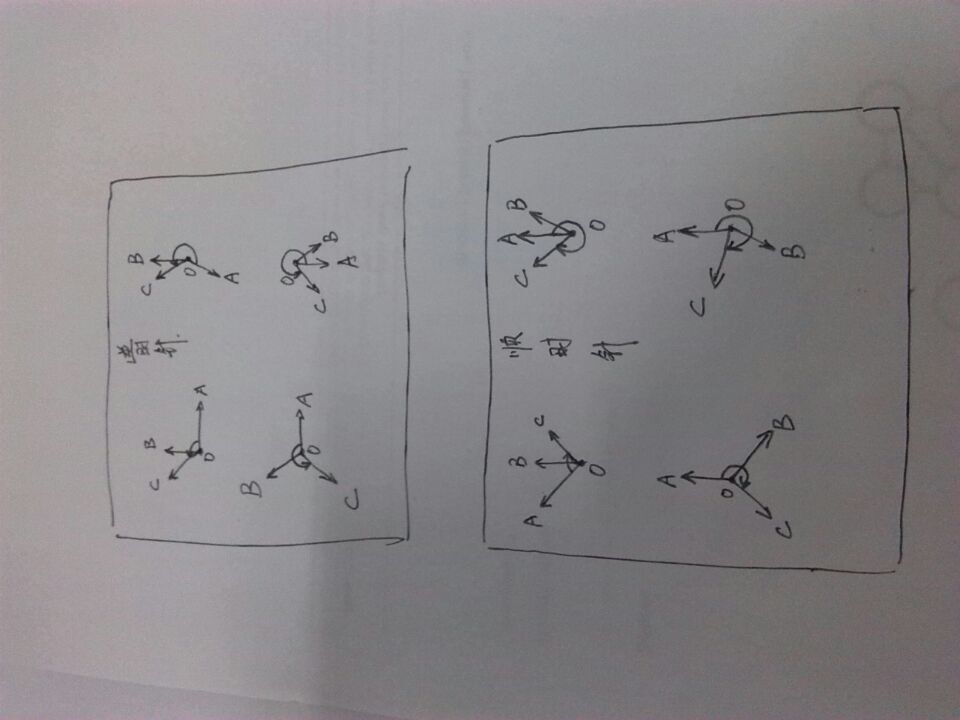
         if(Cross(OA,OB)<=&&Cross(OB,OC)<=||Cross(OA,OB)>=&&Cross(OB,OC)<&&Cross(OA,OC)>||Cross(OA,OB)<&&Cross(OB,OC)>=&&Cross(OA,OC)>)//顺
         {
             if(Cross(OA,OD)<=&&Cross(OD,OC)<=||Cross(OA,OD)>=&&Cross(OD,OC)<&&Cross(OA,OC)>||Cross(OA,OD)<&&Cross(OD,OC)>=&&Cross(OA,OC)>)
             {
                 len=fabs(length(D-O));
                 if(len<=CC.r) len=CC.r-len;
                 else len=len-CC.r;
             }
             else
             {
                 len=min(fabs(length(A-D)),fabs(length(C-D)));
             }
         }
         else if(Cross(OA,OB)>=&&Cross(OB,OC)>=||Cross(OA,OB)>&&Cross(OB,OC)<=&&Cross(OA,OC)<||Cross(OA,OB)<=&&Cross(OB,OC)>&&Cross(OA,OC)<)//逆
         {
             if(Cross(OA,OD)>=&&Cross(OD,OC)>=||Cross(OA,OD)>&&Cross(OD,OC)<=&&Cross(OA,OC)<||Cross(OA,OD)<=&&Cross(OD,OC)>&&Cross(OA,OC)<)
             {
                 len=fabs(length(D-O));
                 if(len<=CC.r) len=CC.r-len;
                 else len=len-CC.r;
             }
             else
             {
                 len=min(fabs(length(A-D)),fabs(length(C-D)));
             }
         }

         printf("Case %d: %0.3f\n",ca++,len);
     }
     return ;
 }
 /*
 0 0 1 1 2 0 1 -1
 3 4 0 5 -3 4 0 1
 0 0 1 1 1 -1 0 -1
 */