Nowcoder | [题解-N210]牛客OI月赛2-提高组

比赛连接戳这里^_^
我才不会说这是我出的题(逃)
周赛题解\((2018.10.14)\)
\(T1\)
\(25\sim50\)分做法\(:\)直接爆搜
作为一个良心仁慈又可爱的出题人当然\(T1\)要送分啦\(qwq\)
\(100\)分做法\(:\)
其实只需要看左上角就行了,因为题目描述写的很清楚,三个人的操作都是为了BLUESKY007能赢,所以游戏一定会结束,那么当横纵坐标最大的非\(B\)颜色方格变为\(B\)颜色时,可操作的方格范围显然是趋向收敛的,又因为操作规则的要求,左上角的方格在每次操作中都会按规则进行变换,当可操作范围收敛到左上角且左上角变为\(B\)颜色时,游戏结束,所以无论中间的操作是怎样进行的,最终左上角的方格一定会变为\(B\)颜色,而且进行操作的人数和操作变换长度相同,所以我们只需要判断左上角方格的颜色即可.

\(T2\)
\(10\)分做法\(:\)特判输出
毕竟数据范围给的那么小,\(n,m\)都\(\leq5\),显然是送分的啊\(qwq\)
\(20\)分做法\(:\)爆搜
就是很裸的爆搜,连优化剪枝之类的高级操作都不需要.但是为什么\(\min(n,m)\leq3\)?这个看下面证明就知道了\(qwq\)
\(100\)分做法\(:\)结论
我们不妨设\(n\)为长,\(m\)为宽

• \(m\leq2:\)显然对于任何一个位置,在图中都不存在另外一个位置使得两者之间相互可达,所以此时\(n\times m\)的所有位置都可以放置,此时答案为\(n\times m\)
• \(m=3:\)对于一个\(3\times n\)的图,其中对于第二行的所有点,在图中都不存在另外一个位置使得两者之间相互可达,所以第二行所有位置都可以放置,对于另外两行我们可以发现,\((1,1)\)和\((3,4)\)只能有一个位置放置,\((1,2)\)和\((3,5)\),\((1,3)\)和\((3,6)\),\((3,1)\)和\((1,4)\),\((3,2)\)和\((1,5)\),\((3,3)\)和\((1,6)\)同理.于是当我们最大化放置个数时,每相邻的六列的放置总是相同的且任意相邻六列至多可以放置\(12\)个,所以当我们按如图所示的方式开始时会达到最大值,此时答案为\(n+6\times\lfloor\frac{n}{6}\rfloor+2\times\min(n\%6,3)\)
  
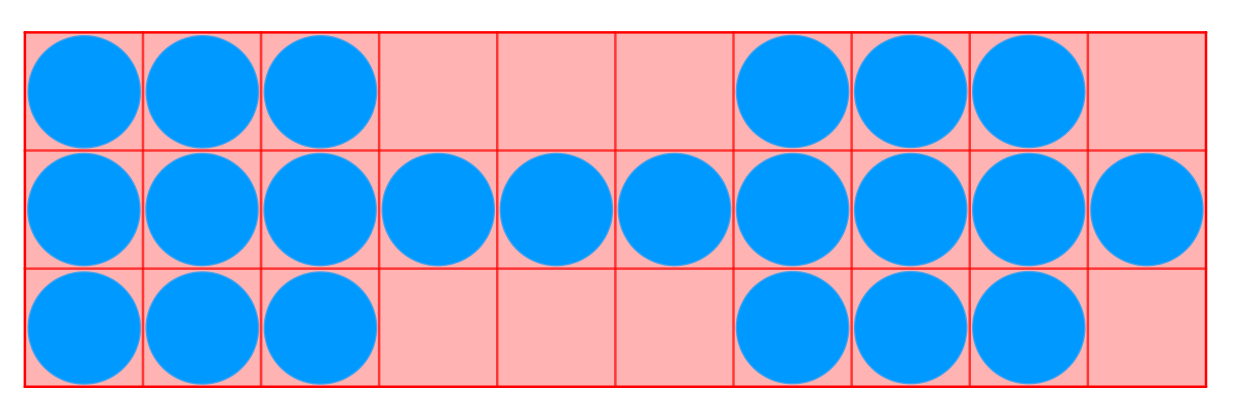
• \(m=4:\)同样的,对于一个\(4\times n\)的图,仍然满足相邻六列最多放置\(12\)个,但是对于不同的\(n\)存在不同的起始方案\(:\)
  • \(n\%6=0:\)从任意列开始,此时答案为\(2n\)
  • \(n\%6\in[1,2]:\)从第\(1\)列开始,此时答案为\(2n+2\times(n\%6)\)
  • \(n\%6\in[3,4]:\)从第\(6\)列开始,此时答案为\(2n+4\)
  • \(n\%6=5:\)从第\(6\)列开始,此时答案为\(12\lceil\frac{n}{6}\rceil\)
    所以如果\(m=4\),能考虑到以上情况的话自然就不是写爆搜的了,所以对爆搜的数据范围设置为\(m\leq3\),否则会\(WA\)

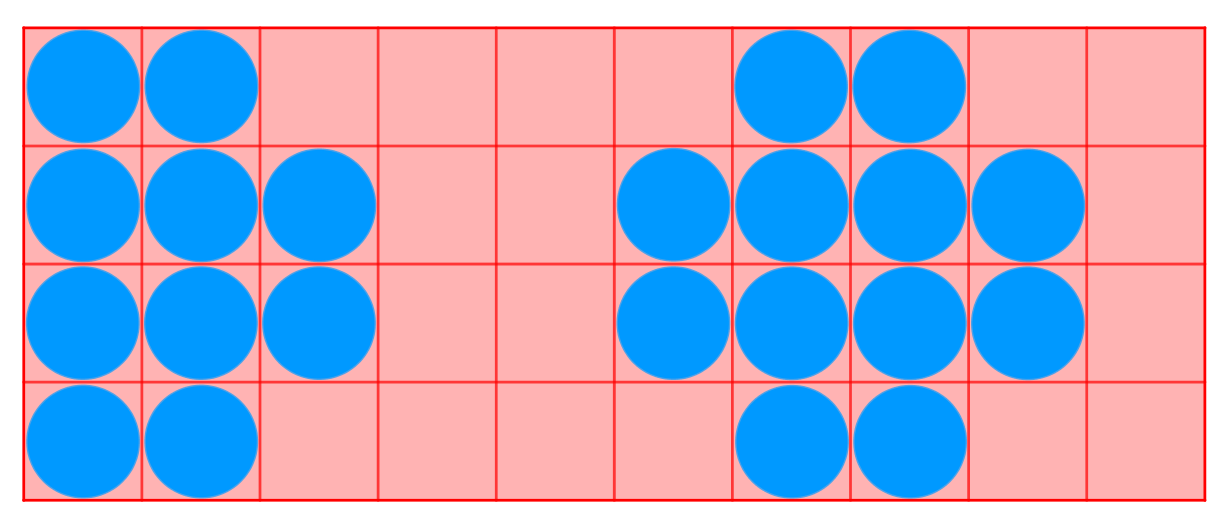
• \(m\geq5:\)如图为\(n=7,m=5\)时的放置方案,类似的,对于任意大小的图都可以进行类似的放置,此时答案为\(\lceil\frac{mn}{2}\rceil\)
  \[
  \begin{vmatrix}
  1&0&1&0&1&0&1\\
  0&1&0&1&0&1&0\\
  1&0&1&0&1&0&1\\
  0&1&0&1&0&1&0\\
  1&0&1&0&1&0&1\\
  \end{vmatrix}
  \]

\(T3\)
\(20\)分做法\(:\)直接输出\(0\)
根据样例解释,\([0,1000]\)内不存在"好朋友",所以对于\(20\%\)数据\(l_i\leq r_i\leq10^3\)显然其中所有的询问答案均为\(0\),所以直接输出就能骗到\(20\)分
\(40\)分做法\(:O(tr\lg(r))\)逐个检验
\(100\)分做法\(:O(t\lg(r))\)数位\(DP\)
因为"好朋友"的定义为含有"007",所以有很多情况都会被视为含有"007",例如"10707","17007"等,此时我们发现对于含有"007"的情况的讨论比较复杂,所以我们不妨讨论不含"007"的情况,也即对于任意的含有\(7\)的数,其中每一个\(7\)前都至多有\(2\)个\(0\),由此可以设\(f_{ij}\)表示在前\(i\)位有\(j\)个\(0\)的数的个数,在数位\(DP\)过程中存当前位置和已有的\(0\)的个数,显然在\(0\)的个数\(\geq2\)时,后面的数位上都不可能再有\(7\).在求出不含"007"的数之后,用区间\(l_i,r_i\)上数的个数减去不含"007"的数的个数即可得到在\(l_i,r_i​\)上含有"007"的数的个数