状压DP概念 及例题（洛谷 P1896 互不侵犯）

状压DP 就是状态压缩DP。所谓状态压缩，就是将一些复杂的状态压缩起来，一般来说是压缩为一个二进制数，用01来表示某一元素的状态。

比如一排灯泡（5个） 我们可以用一串二进制01串来表示他们的状态 11111就是全开 00000就是全关 00001就是只开了第五个 00101就是第三和第五个开了 以此类推.....而这个二进制串是可以用一个十进制数表示的 比如31就是11111 ，1就是00001等等，这样我们在遍历的时候就不用将五个灯泡疯狂循环，只需要从0遍历到31即可 大大节省了时空。

这里需要解释的是，空间的节省是很显然的，本来需要开一个a[5]的数组来存这些灯泡的一种状态，现在只需要一个数了，但是时间复杂度是怎么体现的呢？明明都是2^5种情况呀！似乎并没有节省遍历带来的时间复杂度......这是因为对于二进制的操作要比通过对存储的状态进行模拟简单得多 举个例子来说：假如我们要求这些灯泡相邻的不能同时亮，如果没有用到状压，就是对每种状态进行判断，如果相邻的状态一样就跳出，那么每种状态都需要从1到5扫一遍，这是很麻烦的，但是经过状压之后，这就容易许多了：x&(x<<1) 即可，比之前的方式省时省力！

需要强调的是，状压本身对于dp没有影响，该怎么dp还是怎么dp，但是对于遍历和操作却方便了很多。

下面列出一些二进制的常规操作（江苏省淮阴中学薛志坚整理）

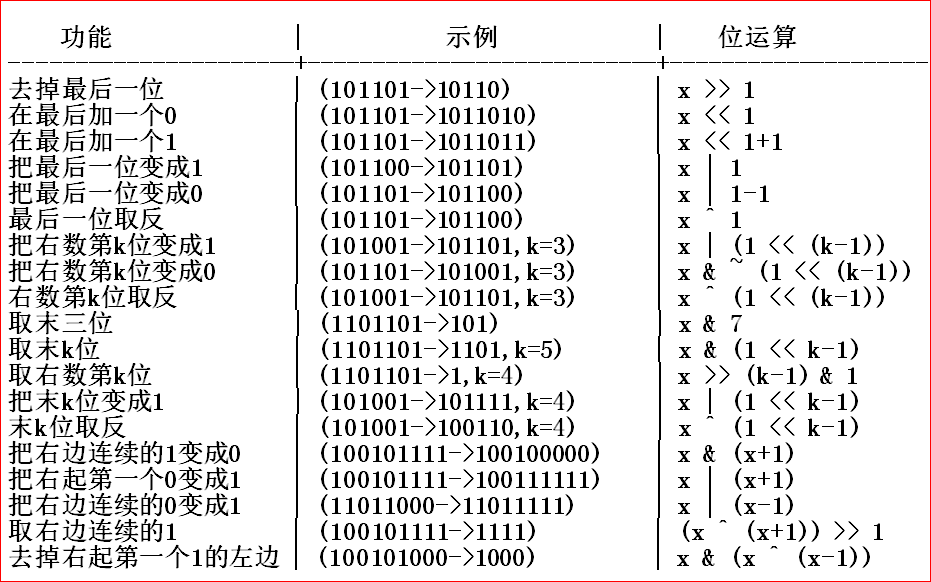
还有求当前二进制串中1的数量 这个是我写这个博客的时候看到的

int sum=;
    while(x){
        ++sum;
        x&=x-;
    }

例题

P1896 [SCOI2005]互不侵犯

我们采用dp[i][j][s]来表示第i行的状态是j的情况下 前i行放了s个国王的方法总数 很明显，dp[i][j][s]+=dp[i-1][k][s-sum(j)] 其中k代表上一行的状态，sum(j)代表第i行的国王数。

具体来看代码：

#include<bits/stdc++.h>

using namespace std;

long long int sit,i,N,K,j,k,s,n,dp[][<<][],a[<<],anss;

long long int sum(long long int i)  //求状态i的国王数
{
    long long int a=;
    while(i)
    {
        if(i&)
        a++;
        i=i>>;
    }
    return a;
}

int main()
{
    cin>>N>>K;
    n=<<N;
    for(i=;i<n;i++)
    {
        if(i&(i<<))    //判断左右国王是否冲突
        continue;
        a[++sit]=i;
        dp[][sit][sum(i)]=;  //初始化
    }
    for(i=;i<=N;i++)
    {
        for(k=;k<=sit;k++)   //上一行
        {
            for(j=;j<=sit;j++)   //本行
            {
                if(a[k]&a[j])  //上下有国王冲突
                continue;
                if(a[k]&(a[j]<<))  //右上有国王冲突
                continue;
                if(a[k]&(a[j]>>))   //左上有国王冲突
                continue;
                for(s=K;s>=sum(a[j])+sum(a[k]);s--)   //遍历前i行放置的国王总数 这里我看的其他博客上写的都是 s>=sum(a[j]) 但是我感觉不需要 因为你得满足前一行的状态　　　　
                dp[i][j][s]+=dp[i-][k][s-sum(a[j])];
            }
        }
    }
    for(i=;i<=sit;i++)
    anss+=dp[N][i][K]; //遍历最后一行的状态 输出答案
    cout<<anss<<endl;
}

需要注意的是 要用 long long 否则是70分......