MIT线性代数:22.对角化和A的幂

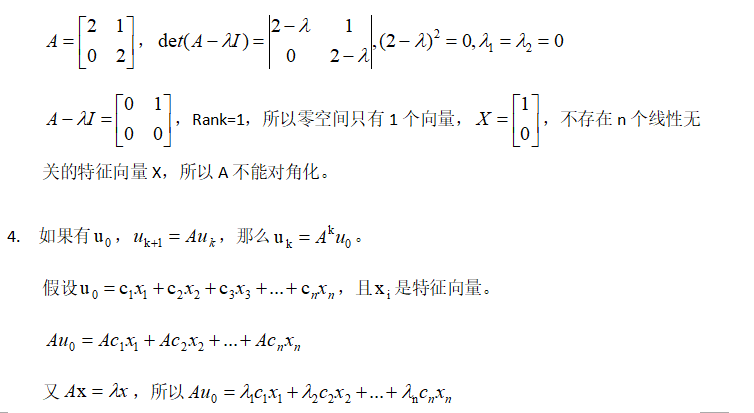
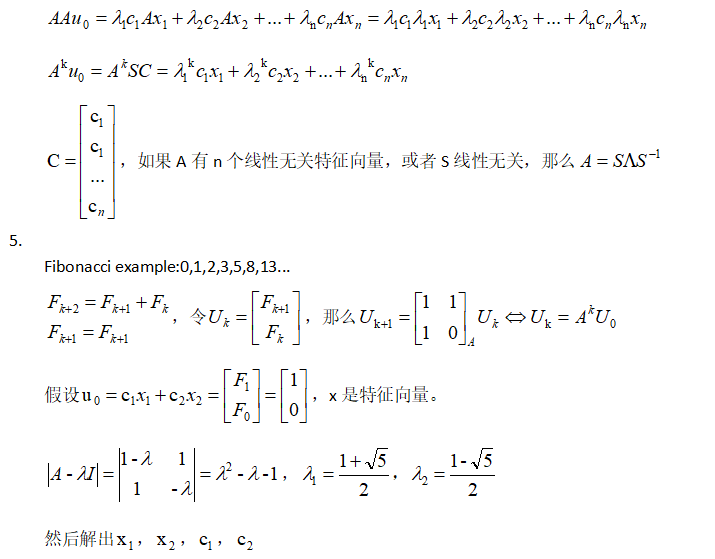
MIT线性代数:22.对角化和A的幂的更多相关文章
- 线性代数之——对角化和 A 的幂
利用特征向量的属性,矩阵 \(A\) 可以变成一个对角化矩阵 \(\Lambda\). 1. 对角化 假设一个 \(n×n\) 的矩阵 \(A\) 有 \(n\) 个线性不相关的特征向量 \(x_1, ...
- MIT线性代数课程 总结与理解-第一部分
概述 个人认为线性代数从三个角度,或者说三个工具来阐述了线性关系,分别是: 向量 矩阵 空间 这三个工具有各自的一套方法,而彼此之间又存在这密切的联系,通过这些抽象出来的工具可以用来干一些实际的活,最 ...
- MIT线性代数:21.特征值和特征向量
- MIT线性代数:20.克拉默法则,逆矩阵和体积
- MIT线性代数:19.行列式和代数余子式
- MIT线性代数:18.行列式及其特性
- MIT线性代数:17.正交矩阵和Cram-Schmidt正交化
- MIT线性代数:16.投影矩阵和最小二乘
- MIT线性代数:15.子空间的投影
随机推荐
- raspbian修改swap分区为硬盘上的分区
一直以为raspbian的swap分区和平常装系统时候的swap分区是一样的,最近用u盘插在树莓派上运行后发现这个交换分区和我想象中不一样. 百度后发现它是一个文件挂上去的.直接搞把! pi@rasp ...
- 网络下载器 Internet Download Manager v6.35.5 绿色便携版
Internet Download Manager,简称 IDM,是国外的一款优秀网络下载工具.目前凭借着下载计算的速度优势在外媒网站中均受好评,现在已被多数国人熟知.Internet Downloa ...
- 想转行做3D游戏模型,如何快速入行
随着技术和硬件迭代,3D建模,广泛运用在游戏,影视,动画,VR等领域,而且就业面非常广. 由于3D美术设计师薪资和前景确实都不错,很多同学想进入这个行业,从事相关工作,但是没有一个整体的学习思路和规划 ...
- Python3实战spark大数据分析及调度 ☝☝☝
Python3实战spark大数据分析及调度 ☝☝☝ 一.实例分析 1.1 数据 student.txt 1.2 代码 二.代码解析 2.1函数解析 2.1.1 collect() RDD的特性 在 ...
- Vue-cli中的跳转
Vue-cli中的跳转 一.页面中跳转指定网页 写法一: <router-link :to="{name:'home'}"> 这里的name是在VUE路由里面的 写法二 ...
- ARM64架构下,OpenJDK的官方Docker镜像为何没有8版本
为什么需要ARM64架构的OpenJDK8的Docker镜像 对现有的Java应用,之前一直运行在x86处理器环境下,编译和运行都是JDK8,如今在树莓派的Docker环境运行(也可能是其他ARM环境 ...
- RAW网络编程
LWIP提供了三种的可以被应用程序直接调用的接口API: (1) 低水平的,基于内核/回调函数的API(后面称 RAW API) 适用于数据量不大,没有os的MCU (2) ...
- L2-007. 家庭房产(并查集)
#include <cstdio> #include <set> #include <vector> #include <algorithm> usin ...
- Js极客之路 - 优化操作(性能优化)
1.因为每次For循环都会计算一次arr.length,所以有必要存储数组长度以减少计算.针对这篇文章(http://www.crimx.com/2015/04/21/should-array-len ...
- Easy Poi入门
最近有一个需求,就是把excel中的内容,解析成Json对象格式的文件输出. 然后就上网找了一波资料,大神们都说用POI来做.但是我看了一下POI的解析过程,但是为了秉着高效的原则,花最少的时间去实现 ...
