C++动态规划求解0-1背包问题

问题描述：

给定n种物品和一背包。物品i的重量是w_i，其价值为v_i，背包的容量为C。问：应该如何选择装入背包的物品，是的装入背包中物品的总价值最大？

细节须知：

暂无。

算法原理：

a.最优子结构性质

0-1背包问题具有最优子结构性质。设（y₁，y₂，…，y_n）是所给0-1背包问题的一个最优解，则（y₂，…，y_n）是下面相应子问题的一个最优解。

b.递归关系

设所给0-1背包问题的子问题

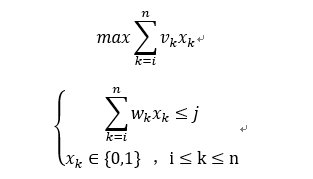
的最优值为m（i，j），即m（i，j）是背包容量为j，可选择物品为i，i+1，…，n时0-1背包问题的最优值。有0-1背包问题的最优子结构性质，可以建立如下计算m（i，j）的递归式

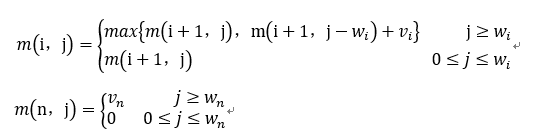
 #include <iostream>
 #include <fstream>
 #include <ctime>
 #include <algorithm>
 #include <windows.h>
 using namespace std;
 #define N 10000

 //int w[5] = { 0 , 2 , 3 , 4 , 5 };            //商品的体积2、3、4、5
 //int v[5] = { 0 , 3 , 4 , 5 , 6 };            //商品的价值3、4、5、6
 //int bagV = 8;                            //背包大小
 int dp[N][N];                    //动态规划表
 //int item[5];                            //最优解情况

 void findMax(int k,int n,int w[],int v[]) {                    //动态规划
     for (int i = ; i <= k; i++) {
         for (int j = ; j <= n; j++) {
             if (j < w[i])
                 dp[i][j] = dp[i - ][j];
             else
                 dp[i][j] = max(dp[i - ][j], dp[i - ][j - w[i]] + v[i]);
         }
     }
 }

 void findWhat(int i, int j,int w[],int v[],int item[]) {                //最优解情况
     if (i > ) {
         if (dp[i][j] == dp[i - ][j]) {
             item[i] = ;
             findWhat(i - , j,w,v,item);
         }
         else if (j - w[i] >=  && dp[i][j] == dp[i - ][j - w[i]] + v[i]) {
             item[i] = ;
             findWhat(i - , j - w[i],w,v,item);
         }
     }
 }

 void print(int k,int n,int item[]) {
     /*for (int i = 0; i < k+1; i++) {            //动态规划表输出
         for (int j = 0; j < n+1; j++) {
             cout << dp[i][j] << ' ';
         }
         cout << endl;
     }
     cout << endl;*/
     cout <<"The item number that should be put into the backpack is:";
     for (int i = ; i < k+; i++){            //最优解输出
         if(item[i] == )
           cout << i << ' ';
     }
     cout << endl;
 }

 int main(void)
 {
     LARGE_INTEGER nFreq;
     LARGE_INTEGER nBeginTime;
     LARGE_INTEGER nEndTime;
     ofstream fout;
     double cost;
     int i,j,m,n,k;
     cout << "Please enter the number of times you want to run the program:";
     cin >> m;
     //int object_amount[m];
     //double runtime[m];
     fout.open("backpack.txt",ios::app);
     if(!fout){
         cerr<<"Can not open file 'backpack.txt' "<<endl;
         return -;
     }
     fout.setf(ios_base::fixed,ios_base::floatfield);       //防止输出的数字使用科学计数法
     srand((unsigned int)time(NULL));
     for(i = ; i < m; i++){
         n = rand()%;
         k = rand()%;
         //object_amount[i] = k;
         fout<<k<<",";
         int item[k];
         cout << "The " << i+ << "th test's backpack lattice number is:" << n << endl;
         cout << "The " << i+ << "th test's object amount is:" << k << endl;
         int w[k];
         int v[k];
         memset(dp,,sizeof(dp));
         w[] = ;
         v[] = ;
         for(j=;j<k;j++){
             w[j]=rand()%;
             v[j]=rand()%;
         }
         QueryPerformanceFrequency(&nFreq);
         QueryPerformanceCounter(&nBeginTime);
         findMax(k,n,w,v);
         findWhat(k,n,w,v,item);
         print(k,n,item);
         QueryPerformanceCounter(&nEndTime);
         cost=(double)(nEndTime.QuadPart - nBeginTime.QuadPart) / (double)nFreq.QuadPart;
         //runtime[i]=cost;
         fout<<cost<<endl;
         cout<<"The running time is:"<<cost<<" s"<<endl;
     }
 /*    fout.open("backpack.txt",ios::app);
     if(!fout){
         cerr<<"Can not open file 'backpack.txt' "<<endl;
         return -1;
     }
     fout.setf(ios_base::fixed,ios_base::floatfield);       //防止输出的数字使用科学计数法
     for(i=0;i<m;i++){
            fout<<object_amount[i]<<","<<runtime[i]<<endl;
     }*/
     fout.close();
     cout<<"Success!"<<endl;
     return ;
 }

程序设计思路：

根据算法原理中所述递归关系，递归计算全部的m（i，j），得到不同情况下的最优解。

假设m[1][c]给出所要求的的0-1背包问题的最优值。相应的最优解计算如下：

如果m[1][c]=m[2][c]，则x₁=0；否则x₁=1.当x₁=0是，由m[2][c]继续构造最优解；当x₁=1时，有m[2][c-w₁]继续构造最优解。以此类推，可构造出相应的最优解（x₁，x₂，…，x_n）。

时间复杂性分析：

从计算m（i，j）的递归式容易看出，对于0-1背包问题的求解算法需要O（nc）计算时间，而算法解出最优方案需要O（n）计算时间，当背包容量c很大时，算法需要的计算时间较多。

生成的数据可导入EXCEL中进行数据分析生成分析图表。