洛谷 P2996 [USACO10NOV]拜访奶牛Visiting Cows

P2996

传送门

题意：

给你一棵树，每一条边上最多选一个点，问你选的点数.

我的思想：

一开始我是想用黑白点染色的思想来做，就是每一条边都选择一个点.

可以跑两边一遍在意的时候染成黑，第二遍染成白,取一个最大值.

就可以得到\(30\)分的高分.

#include <bits/stdc++.h>
#define N 100010
#define M 1010
#define _ 0

using namespace std;
int n, tot, ans, add_edge, color[N], head[N];
struct node {
	int next, to;
}edge[N];

int read() {
	int s = 0, f = 0; char ch = getchar();
	while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
	while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
	return f ? -s : s;
}

void add(int from, int to) {
	edge[++add_edge].next = head[from];
	edge[add_edge].to = to;
	head[from] = add_edge;
}

void dfs(int x, int fx) {
	if (color[fx] == 0) {
		color[x] = 1;
		tot++;
	}
	for (int i = head[x]; i; i = edge[i].next) {
		int to = edge[i].to;
		if (to == fx) continue;
		dfs(to, x);
	}
}

int main() {
	n = read();
	int point;
	for (int i = 1, x, y; i < n; i++) {
		x = read(), y = read();
		add(x, y), add(y, x);
		point = x;
	}
	dfs(point, 0);
	ans = max(ans, tot);
	memset(color, 0, sizeof (color));
	tot = 0, color[0] = 1;
	dfs(point, 0);
	cout << max(ans, tot);
}

很明显这样做是错误的.来看这样一组样例.



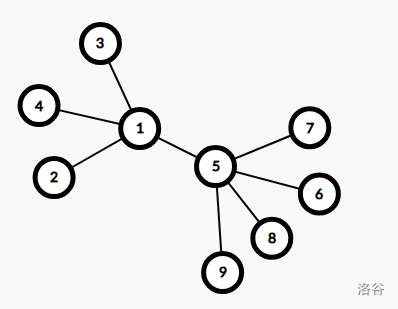
按照上述方法跑出来就是\(5\)，显然答案是\(7\).然后我就是这样被学长\(hack\)了.

然后就问了学长树形\(DP\).

正确思路:

我们设\(dp[i][1/0]\)来表示\(i\)与\(i\)的子树在\(i\)，选还是不选，时的最大权值.

然后又因为在\(dp[i][1]\)时他的子节点不能选\(dp[to][1]\).

在\(dp[i][0]\)时都可以选.我们就可以得到这样的转移方程(用\(to\)来表示\(i\)的子节点)：

\[dp[x][0] += max(dp[to][1], dp[to][0]);
\]

\[dp[x][1] += dp[to][0];
\]

然后就做完了.

code :

#include <bits/stdc++.h>
#define N 100010
#define M 50010
#define _ 0

using namespace std;
int n, add_edge, head[N];
int dp[M][2];
struct node {
	int next, to;
}edge[N];

int read() {
	int s = 0, f = 0; char ch = getchar();
	while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
	while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
	return f ? -s : s;
}

void add(int from, int to) {
	edge[++add_edge].next = head[from];
	edge[add_edge].to = to;
	head[from] = add_edge;
}

void dfs(int x, int fx) {
	dp[x][1] = 1;
	for (int i = head[x]; i; i = edge[i].next) {
		int to = edge[i].to;
		if (to == fx) continue;
		dfs(to, x);
		dp[x][0] += max(dp[to][1], dp[to][0]);
		dp[x][1] += dp[to][0];
	}
}

int main() {
	n = read();
	for (int i = 1, x, y; i < n; i++) {
		x = read(), y = read();
		add(x, y), add(y, x);
	}
	dfs(1, 0);
	cout << max(dp[1][0], dp[1][1]);
}