Leetcode 207.课程表

课程表

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，判断是否可能完成所有课程的学习？

示例 1:

输入: 2, [[1,0]]

输出: true

解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。

示例 2:

输入: 2, [[1,0],[0,1]]

输出: false

解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。

说明:

1. 输入的先决条件是由边缘列表表示的图形，而不是邻接矩阵。详情请参见图的表示法。
2. 你可以假定输入的先决条件中没有重复的边。

拓扑排序

对一个有向无环图G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v,若存在由 u 到 v的路径，则在拓扑排序序列中一定是 u 出现在 v 的前边。

在一个有向图中找到一个拓扑排序序列的过程如下：

从有向图中选择一个没有前驱（入度为0）的顶点输出。

删除1. 中的顶点，并且删除从该顶点出发的全部边。

重复上述两步，直到剩余的网中不存在没有前驱的顶点为止。

可以利用宽度优先遍历的思想完成。

设置一个count 记录输出的顶点个数，用一个队列记得当前入度为0的结点。

从入度为 0 的结点入队。然后队列不空的时候循环执行，出队，将出队顶点输出，count++,将由此顶点引出的边所指向的顶点的入度都减1，并且将入度变成0的顶点入队，队列为空退出，排序结束。判断n是否等于图中顶点个数，如果等于，排序成功。

图的存储结构：

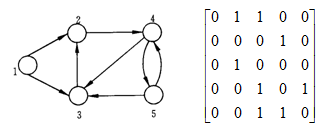
1、邻接矩阵表示法：

如果 第 1个点和第 3个点 相连则 matrix[0][2]=1;如果两节点之间有一条弧，则邻接矩阵中对应的元素为1；否则为0。可以看出，这种表示法非常简单、直接。但是，在邻接矩阵的所有n*n 个元素中，只有 m个为非零元。如果网络比较稀疏，这种表示法浪费大量的存储空间，从而增加了在网络中查找弧的时间。

这里写图片描述

2、邻接表表示法：

邻接表表示法将图以邻接表（adjacency lists）的形式存储在计算机中。所谓图的邻接表，也就是图的所有节点的邻接表的集合；而对每个节点，它的邻接表就是它的所有出弧。邻接表表示法就是对图的每个节点，用一个单向链表列出从该节点出发的所有弧，链表中每个单元对应于一条出弧。为了记录弧上的权，链表中每个单元除列出弧的另一个端点外，还可以包含弧上的权等作为数据域。图的整个邻接表可以用一个指针数组表示。

这里写图片描述

 class Solution {
     public boolean canFinish(int numCourses, int[][] prerequisites) {
         int[][] matrix = new int[numCourses][numCourses]; // i -> j //邻接矩阵存储图
         int[] indegree = new int[numCourses]; // 统计每个节点的入度
         for (int i = 0; i < prerequisites.length; i++) {
             int ready = prerequisites[i][0];
             int pre = prerequisites[i][1];
             if (matrix[pre][ready] == 0)
                 indegree[ready]++; matrix[pre][ready] = 1;
         }
         int count = 0;
         Queue<Integer> queue = new LinkedList();
         for (int i = 0; i < indegree.length; i++) {
             if (indegree[i] == 0) queue.offer(i);
         }
         while (!queue.isEmpty()) {
             int course = queue.poll();
             count++;
             for (int i = 0; i < numCourses; i++) {
                 if (matrix[course][i] != 0) {// 节点 i 与该节点相连
                     indegree[i]--;
                     // 与刚出队的节点相连的节点，入度减一
                     if (indegree[i] == 0) {
                         // 如果为0，说明没有前驱，可以访问
                         queue.offer(i);
                     }
                 }
             }
         }
         return count == numCourses; // 如果所有节点是否都访问了，如果是说明成功
     }
 }