cf 337 div2 c

C. Harmony Analysis

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The semester is already ending, so Danil made an effort and decided to visit a lesson on harmony analysis to know how does the professor look like, at least. Danil was very bored on this lesson until the teacher gave the group a simple task: find 4 vectors in 4-dimensional space, such that every coordinate of every vector is 1 or  - 1 and any two vectors are orthogonal. Just as a reminder, two vectors in n-dimensional space are considered to be orthogonal if and only if their scalar product is equal to zero, that is:

.

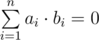Danil quickly managed to come up with the solution for this problem and the teacher noticed that the problem can be solved in a more general case for 2k vectors in 2k-dimensinoal space. When Danil came home, he quickly came up with the solution for this problem. Can you cope with it?

Input

The only line of the input contains a single integer k (0 ≤ k ≤ 9).

Output

Print 2k lines consisting of 2k characters each. The j-th character of the i-th line must be equal to ' * ' if the j-th coordinate of the i-th vector is equal to  - 1, and must be equal to ' + ' if it's equal to  + 1. It's guaranteed that the answer always exists.

If there are many correct answers, print any.

Sample test(s)

input

2

output

++**
+*+*
++++
+**+

Note

Consider all scalar products in example:

• Vectors 1 and 2: ( + 1)·( + 1) + ( + 1)·( - 1) + ( - 1)·( + 1) + ( - 1)·( - 1) = 0
• Vectors 1 and 3: ( + 1)·( + 1) + ( + 1)·( + 1) + ( - 1)·( + 1) + ( - 1)·( + 1) = 0
• Vectors 1 and 4: ( + 1)·( + 1) + ( + 1)·( - 1) + ( - 1)·( - 1) + ( - 1)·( + 1) = 0
• Vectors 2 and 3: ( + 1)·( + 1) + ( - 1)·( + 1) + ( + 1)·( + 1) + ( - 1)·( + 1) = 0
• Vectors 2 and 4: ( + 1)·( + 1) + ( - 1)·( - 1) + ( + 1)·( - 1) + ( - 1)·( + 1) = 0
• Vectors 3 and 4: ( + 1)·( + 1) + ( + 1)·( - 1) + ( + 1)·( - 1) + ( + 1)·( + 1) = 0

假设把当前2 ^ k * (2 ^ k)分成左上，右上，左下，右下四个方阵，假设当前我们已知k - 1时的方阵，只要把左上，左下右上填成与k - 1相同方阵，右下填成

　 与k - 1方阵反相即可。

　　

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <cmath>
 
 using namespace std;
 
 const int maxn = ;
 char mar[maxn][maxn];
 int k;
 
 char invert(char x) {
     return x == '+' ? '*' : '+';
 }
 
 int main() {
     scanf("%d", &k);
     mar[][] = '+';
     for (int i = ; i <= k; ++i) {
         int a = pow(, i - );
         int b = pow(, i);
         for (int r = ; r < a; ++r) {
             for (int c = a; c < b; ++c) {
                 mar[r][c] = mar[r][c - a];
             }
         }
 
         for (int r = a; r < b; ++r) {
             for (int c = ; c < a; ++c) {
                 mar[r][c] = mar[r - a][c];
             }
         }
 
         for (int r = a; r < b; ++r) {
             for (int c = a; c < b; ++c) {
                 mar[r][c] = invert(mar[r][c - a]);
             }
         }
     }
 
     int a = pow(, k);
     for (int i = ; i < a; ++i) {
         for (int j = ; j < a; ++j) {
             printf("%c", mar[i][j]);
         }
         printf("\n");
     }
 
     return ;
 }