「 RQNOJ PID204 」 特种部队

解题思路

看了一下题解，感觉题解貌似有些错误。所以把我的见解放在这里，希望路过的大佬可以帮忙解释一下 QAQ

就是这里的更新 $dp[i-1][i]$ 和 $dp[i][i-1]$ 的时候，之前博主说的是 $dp[i][j]$ 表示第一条路走到了i第二条路走到了 $j$，并且 $i>j$，且 $1\rightarrow i$上的点都走过了。

那它更新的时候难道不是向下面这样吗

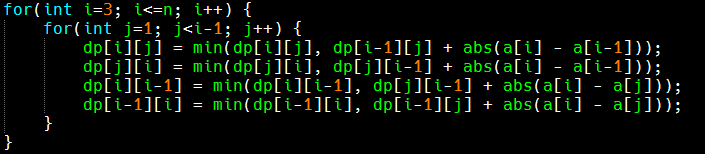
希望大佬能够帮忙解释一下。蟹蟹蟹蟹٩('ω')و

-------------分割线-------------

既然是从起点跑到终点再从终点跑回来。那么就可以将其看作是从终点到出发点 (或者从出发点到终点都一样) 两条完全不重合路径。

设 $dp[i][j]$ 表示第一条路径 (A) 走到了第 $i$ 个点上，第二条路径 (B) 走到了第 $j$ 个点上，并且 $1\rightarrow i$ 这段上和 $1\rightarrow j$ 的所有点都被走过。

那么就会出现下面两种情况 (跳一格还是跳若干格)，这两种情况下又有两种情况 (A 跳还是 B 跳)

• 当前跳的这一步只是跳了一个格子
  • A 上一步在 B 上一步后面 (远) 那么直接就是 A 通过跳一步到达了 $i$，而 B 保持在原地不动。$dp[i][j] = \min \{ dp[i][j],dp[i-1][j]+|dist[i]-dist[j]| \}$
  • A 上一步在 B 上一步前面 (近) 那么就是 B 通过跳一步到达了 $i$，而 A 保持原地不动。$dp[j][i] = \min \{ dp[j][i], dp[j][i-1]+|dist[i]-dist[j]| \}$
• 当前跳的这一步越过了若干格子
  • A 上一步在 B 之前好多个格子，那么 A 直接跳到 $i$，B 保持原地不动。$dp[i][i-1] = \min \{ dp[i][i-1],dp[j][i-1] + |dist[i]-dist[j]| \}$
  • A 上一步在 B 之后好多个格子，那么 B 直接跳到 $i$，A 保持原地不动。$dp[i-1][i] = \min \{ dp[i-1][i],dp[i-1][j] + |dist[i]-dist[j]| \}$

附上代码

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int maxn = ;
int n, a[maxn], dp[maxn][maxn], Ans = ;
inline int abs(int x) {
    return x >  ? x : -x;
}
int main() {
    scanf("%d", &n);
    for(int i=n; i>=; i--)
        scanf("%d", &a[i]);
    memset(dp, 0x7f, sizeof(dp));
    dp[][] = , dp[][] = dp[][] = abs(a[]-a[]);
    for(int i=; i<=n; i++) {
        for(int j=; j<i-; j++) {
            dp[i][j] = min(dp[i][j], dp[i-][j] + abs(a[i] - a[i-]));
            dp[j][i] = min(dp[j][i], dp[j][i-] + abs(a[i] - a[i-]));
            dp[i][i-] = min(dp[i][i-], dp[j][i-] + abs(a[i] - a[j]));
            dp[i-][i] = min(dp[i-][i], dp[i-][j] + abs(a[i] - a[j]));
        }
    }
    for(int i=; i<=n; i++)
        Ans = min(Ans, dp[i][n]);
    printf("%d", Ans);
}