【C++】朝花夕拾——表达式树

表达式树:

　　　　　　　叶子是操作数，其余结点为操作符，是二叉树的其中一种应用

====================我是分割线======================

一棵表达式树如下图：　

　　

　　若是对它做中序遍历，则可以得到中缀表达式

　　　　　　做后序遍历，则可以得到后缀表达式

已知树的结点可以表示成：

 struct TreeNode {
      object element;
      TreeNode* leftChild;
      TreeNode* rightChild;
  };

用后缀表达式构建一棵表达式树：

　　思路：（与后缀表达式计算四则运算结构相似）

　　　　　1. 一一读入输入字符串

　　　　　2. 若是操作数，则初始化为结点后入栈

　　　　　3. 若是操作符，则从栈中弹出两个结点（新结点的左右子树），与刚读入的操作符结合起来构建新结点，然后入栈

　　　　　重复1~3，最后栈内有一棵表达式树的root结点

code实现：

 #include<iostream>
 #include <string>
 #include<stack>

 using namespace std;

 struct TreeNode{
     char element;
     TreeNode* leftChild;
     TreeNode* rightChild;
     TreeNode(char ch, TreeNode* l, TreeNode* r) {
         element = ch;
         leftChild = l;
         rightChild = r;
     }
     TreeNode() {
         element = '';
         leftChild = ;
         rightChild = ;
     }
 };

 //测试函数——输出树
 void drawTree(TreeNode* root, bool infix) {
     if (infix) {
         if (root) {
             //中序遍历
             drawTree(root->leftChild, infix);
             cout << root->element;
             drawTree(root->rightChild, infix);
         }
         else return;
     }
     else {
         if (root) {
             //后序遍历
             drawTree(root->leftChild, infix);
             drawTree(root->rightChild, infix);
             cout << root->element;
         }
         else return;
     }
 }

 int main() {
     string input;
     stack<TreeNode> expressionTree;
     while (cin >> input) {
         if (input == "") break;
         for (int i = ; i < input.size();) {
             char ch = input[i++];
             if (ch >= '' && ch <= '') {
                 TreeNode leaves;
                 leaves.element = ch;
                 expressionTree.push(leaves);
             }
             else {
                 //出栈，成为新结点右子树
                 TreeNode* right = new TreeNode(expressionTree.top().element, expressionTree.top().leftChild, expressionTree.top().rightChild);
                 expressionTree.pop();

                 ////出栈，成为新结点左子树
                 TreeNode* left = new TreeNode(expressionTree.top().element, expressionTree.top().leftChild, expressionTree.top().rightChild);
                 expressionTree.pop();

                 //新结点入栈
                 TreeNode leave(ch, left, right);
                 expressionTree.push(leave);
             }
         }
         TreeNode* root = &expressionTree.top();
         expressionTree.pop();
         drawTree(root, true);
     }
     return ;
 }

 //NULL 与 0 的概念

局限性：

　　1. 假设所有输入合法，无空格等非法符号输入

　　2. 测试输出函数不能还原优先级，12+3* 的表达式树测试输出将是 1+2*3，而并非（1+2）*3，如果需要，可以在结构体中再加上一个优先级判断，若子结点的操作符优先级小于父结点，则输出时子树的表达式需要最后要整体放到一个括号内。

一些bugs:

　　关于NULL、0 和 nullptr的学习：

　　　　1. NULL是宏

　　　　2. C中对于NULL的定义为 #define NULL ((void *)0)

　　　　3. C++中对于NULL的定义为0

　　　　　　#ifdef __cplusplus
　　　　　　#define NULL 0
　　　　　　#else
　　　　　　#define NULL ((void *)0)
　　　　　　#endif

　　　　4. C++11中对于nullptr的定义　　　　　　

 const
 class nullptr_t
 {
 public:
     template<class T>
     inline operator T*() const
         { return ; }

     template<class C, class T>
     inline operator T C::*() const
         { return ; }

 private:
     void operator&() const;
 } nullptr = {};

　　　　

　　　　5. 由于C++中的定义，在重载函数时容易出错

 //NULL  0   nullptr
 #include <iostream>
 #include <stdio.h>

 using namespace std;

 int f(void* ptr) {
     return ;
 }

 int f(int num) {
     return ;
 }

 int main() {
     int result1 = f();
     //int result2 = f(NULL);
     int result3 = f(nullptr);
     cout << "result1 = " << result1 << endl;
     //cout << "result2 = " << result2 << endl;
     cout << "result3 = " << result3 << endl;
     return ;
 }

　　　　当我把17行的注释符去掉时：编译错误

　　　　

　　　　最后运行的结果如下：

　　　　

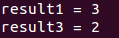
　　　　说明C++11标准中，nullptr的调用在重载时不会又歧义，而0则会在重载时调用int形参的函数

　　　　在C++中，可以的话，尽量用nullptr为空指针赋值

　　　　文章推荐：

　　　　　　http://www.cppblog.com/airtrack/archive/2012/09/16/190828.html