洛谷 P2751 [USACO4.2]工序安排Job Processing 解题报告

P2751 [USACO4.2]工序安排Job Processing

题目描述

一家工厂的流水线正在生产一种产品，这需要两种操作：操作A和操作B。每个操作只有一些机器能够完成。

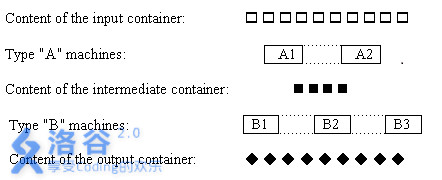
上图显示了按照下述方式工作的流水线的组织形式。A型机器从输入库接受工件，对其施加操作A，得到的中间产品存放在缓冲库。B型机器从缓冲库接受中间产品，对其施加操作B，得到的最终产品存放在输出库。所有的机器平行并且独立地工作，每个库的容量没有限制。每台机器的工作效率可能不同，一台机器完成一次操作需要一定的时间。

给出每台机器完成一次操作的时间，计算完成A操作的时间总和的最小值，和完成B操作的时间总和的最小值。

注：1、机器在一次操作中干掉一个工件； 2、时间总和的意思是最晚时间点

输入输出格式

输入格式：

第一行 三个用空格分开的整数：N，工件数量 (1<=N<=1000);M1，A型机器的数量 (1<=M1<=30);M2，B型机器的数量 (1<=M2<=30)。

第二行…等 M1个整数（表示A型机器完成一次操作的时间，1..20），接着是M2个整数（B型机器完成一次操作的时间，1..20）

输出格式：

只有一行。输出两个整数：完成所有A操作的时间总和的最小值，和完成所有B操作的时间总和的最小值（A操作必须在B操作之前完成）。

输入输出样例

输入样例：

5 2 3

1 1 3 1 4

输出样例：

3 5

---

贪心的题都很神啊。这题耗了我一晚上（我太蒻了）

首先第一问的方法似乎很多，我介绍一下我想的

策略：保证用完某个机器后时间最短

做法：从小到大枚举时间，时间每增加1，对每一个机器的可使用时间就增加1，当一个机器的可使用时间等于它单次操作的时间后，就做并清0

第二问的方法大体有两种，我只弄懂了一种

是一个转换的思想，我们把从B做的操作单独处理，然后用最小-最大进行配对。

具体做法是将B处理按A的方式同样处理，得到每个工件处理完成的时间，然后把A中最小和B中最大取配对并删除，答案即为最大配对值

还有一种大概是直接按时间在B中处理并且用堆维护，看不懂orz

总结：并行取配对，类似的题

---

Code：

#include <cstdio>
int max(int x,int y){return x>y?x:y;}
const int N=32;
int a[N],b[N],n,m1,m2,t1[N],t2[N],put0[1010],put1[1010];
int main()
{
    scanf("%d%d%d",&n,&m1,&m2);
    for(int i=1;i<=m1;i++)
        scanf("%d",t1+i);
    for(int i=1;i<=m2;i++)
        scanf("%d",t2+i);
    int t=0,cnt=n;
    while(cnt)
    {
        t++;
        for(int i=1;i<=m1;i++)
        {
            a[i]++;
            if(a[i]==t1[i]) a[i]=0,put0[cnt--]=t;
            if(!cnt) break;
        }
    }
    printf("%d ",t);
    t=0,cnt=n;
    while(cnt)
    {
        t++;
        for(int i=1;i<=m1;i++)
        {
            b[i]++;
            if(b[i]==t2[i]) b[i]=0,put1[cnt--]=t;
            if(!cnt) break;
        }
    }
    int ans=0;
    for(int i=1;i<=n;i++)
        ans=max(ans,put0[i]+put1[n+1-i]);
    printf("%d\n",ans);
    return 0;
}

---

2018.7.10