POJ 3041&&3020

　　两道二分图的练手题。

　　3041：题意大概是在一个N*N的图上有K个东西，你每次可以清除一行或一列上的所有东西。让你求最少的操作次数。

　　我们根据题意建图。对于每一个点的坐标（x，y）之间连一条边。比如样例：

　　

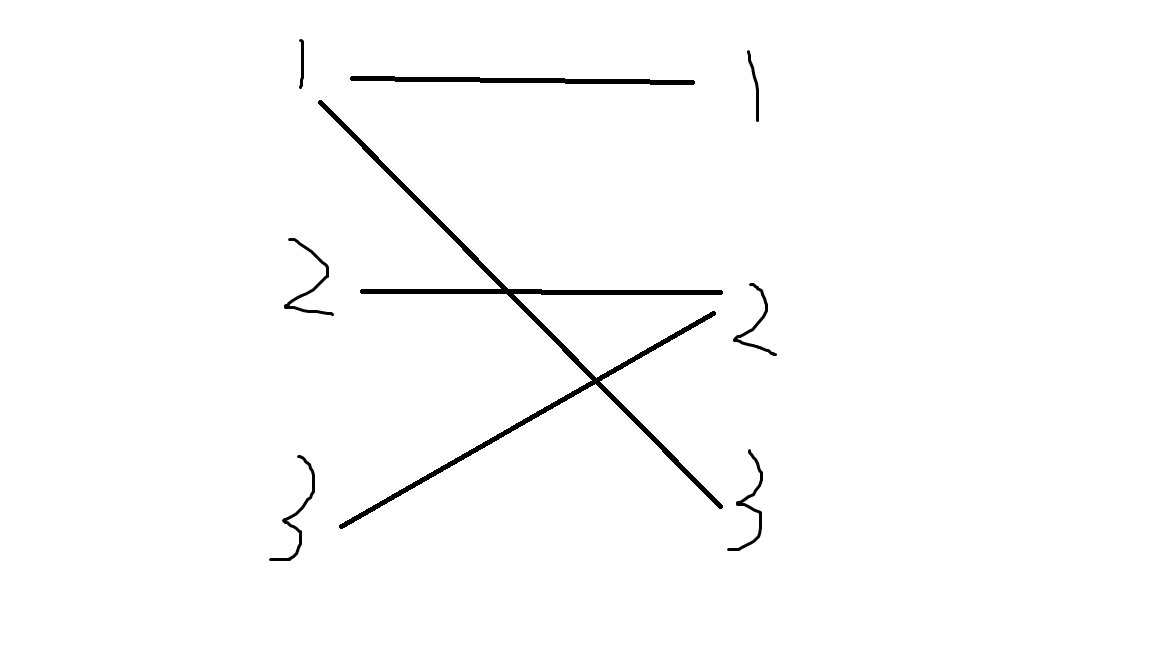
　　由于每条边代表着一个点，因此我们只需要找出最少的点来联结所有的边，也就是最小顶点覆盖=最大匹配

　　CODE

#include<cstdio>
#include<cstring>
using namespace std;
const int K=;
struct data
{
    int to,next;
}e[K];
int head[K],from[K],n,m,x,y,k,i,ans;
bool vis[K];
inline void read(int &x)
{
    x=; char ch=getchar();
    while (ch<''||ch>'') ch=getchar();
    while (ch>=''&&ch<='') x=x*+ch-'',ch=getchar();
}
inline void add(int x,int y)
{
    e[++k].to=y; e[k].next=head[x]; head[x]=k;
}
inline bool find(int now)
{
    for (int i=head[now];i!=-;i=e[i].next)
    if (!vis[e[i].to])
    {
        vis[e[i].to]=;
        if (!from[e[i].to]||find(from[e[i].to]))
        {
            from[e[i].to]=now;
            return ;
        }
    }
    return ;
}
int main()
{
    memset(e,-,sizeof(e));
    memset(head,-,sizeof(head));
    read(n); read(m);
    for (i=;i<=m;++i)
    {
        read(x); read(y);
        add(x,y+n);
    }
    for (i=;i<=n;++i)
    {
        memset(vis,,sizeof(vis));
        ans+=find(i);
    }
    printf("%d",ans);
    return ;
}

　　3020：题意是在一个h*w的图上，每次可以找相邻的（即上下左右四个方向）两个城市（在图中为‘*’），不能重复地建一个信号基站。问最少的建立个数是多少。

　　同理，我们可以找出城市，在相邻的两点之间连边。由于只有两点间能连边，所以这是一个二分图。

　　然后要求覆盖所有的城市，就可以转化成最小边覆盖=节点个数-最大匹配/2（因为建的是无向图）

　　CODE

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int N=,M=,fx[]={,,,-},fy[]={,,-,};
struct data
{
    int to,next;
}e[N*M*];
int head[N*M],from[N*M],a[N][M],n,m,t,i,j,p,k,tot,ans;
bool vis[N*M];
char ch;
inline void add(int x,int y)
{
    e[++k].to=y; e[k].next=head[x]; head[x]=k;
}
inline bool find(int now)
{
    for (int i=head[now];i!=-;i=e[i].next)
    if (!vis[e[i].to])
    {
        vis[e[i].to]=;
        if (!from[e[i].to]||find(from[e[i].to]))
        {
            from[e[i].to]=now;
            return ;
        }
    }
    return ;
}
int main()
{
    scanf("%d",&t);
    while (t--)
    {
        memset(e,-,sizeof(e));
        memset(head,-,sizeof(head));
        memset(a,,sizeof(a));
        memset(from,,sizeof(from));
        scanf("%d%d",&n,&m);
        ans=tot=k=;
        for (i=;i<=n;++i)
        for (j=;j<=m;++j)
        {
            cin>>ch;
            if (ch=='*') a[i][j]=++tot;
        }
        for (i=;i<=n;++i)
        for (j=;j<=m;++j)
        for (p=;p<;++p)
        {
            int x=i+fx[p],y=j+fy[p];
            if (x>&&y>&&x<=n&&y<=m)
            if (a[x][y]) add(a[i][j],a[x][y]);
        }
        for (i=;i<=tot;++i)
        {
            memset(vis,,sizeof(vis));
            ans+=find(i);
        }
        printf("%d\n",tot-ans/);
    }
    return ;
}