B样条

在数学的子学科数值分析里，B-样条是样条曲线一种特殊的表示形式。它是B-样条基曲线的线性组合。B-样条是贝兹（贝塞尔）曲线的一种一般化，可以进一步推广为非均匀有理B样条(NURBS)，使得我们能给更多一般的几何体建造精确的模型。

常数B样条

常数B样条是最简单的样条。只定义在一个节点距离上，而且不是节点的函数。它只是不同节点段（knot span）的标志函数（indicator function）。

线性B样条

线性B样条定义在两个相邻的节点段上，在节点连续但不可微。

三次B样条

一个片断上的B样条的表达式可以写作：

其中S_i是第i个B样条片断而P是一个控制点集，i和k是局部控制点索引。控制点的集合会是的集合，其中是比重，当它增加时曲线会被拉向控制点，在减小时则把曲线远离该点。

片段的整个集合m-2条曲线（）由m+1个控制点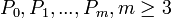（）定义，作为t上的一个B样条可以定义为

其中i是控制点数，t是取节点值的全局参数。这个表达式把B样条表示为B样条基函数的线性组合，这也是这个名称的原因。

有两类B样条-均匀和非均匀。非均匀B样条相邻控制点间的距离不一定要相等。一个一般的形式是区间随着插入控制点逐步变小到0。

关于插值与样条的介绍请看：http://www.cnblogs.com/WhyEngine/p/4020294.html

核心代码：

 void    YcBSpline::BuildWeights()
 {
     ClearWeights();

     for (Yuint i = ; i < ; i++)
     {
         m_splineWeights[i] = (Yreal*)malloc((m_subD)*sizeof(Yreal));
         m_tangentWeights[i] = (Yreal*)malloc((m_subD)*sizeof(Yreal));
     }

     Yreal u, u_2, u_3;
     for (Yuint i = ; i < m_subD; i++)
     {
         u = (float)i / m_subD;
         u_2 = u * u;
         u_3 = u_2 * u;

         // 参见"游戏编程精粹1"P331
         m_splineWeights[][i] = (-1.0f*u_3 + 3.0f*u_2 - 3.0f*u + 1.0f)/6.0f;
         m_splineWeights[][i] = ( 3.0f*u_3 - 6.0f*u_2 + 0.0f*u + 4.0f)/6.0f;
         m_splineWeights[][i] = (-3.0f*u_3 + 3.0f*u_2 + 3.0f*u + 1.0f)/6.0f;
         m_splineWeights[][i] = ( 1.0f*u_3 + 0.0f*u_2 + 0.0f*u + 0.0f)/6.0f;

         // 参见"游戏编程精粹1"P333
         m_tangentWeights[][i] = (-1.0f*u_2 + 2.0f*u - 1.0f)*0.5f;
         m_tangentWeights[][i] = ( 3.0f*u_2 - 4.0f*u + 0.0f)*0.5f;
         m_tangentWeights[][i] = (-3.0f*u_2 + 2.0f*u + 1.0f)*0.5f;
         m_tangentWeights[][i] = ( 1.0f*u_2 + 0.0f*u + 0.0f)*0.5f;
     }
 }

切图：

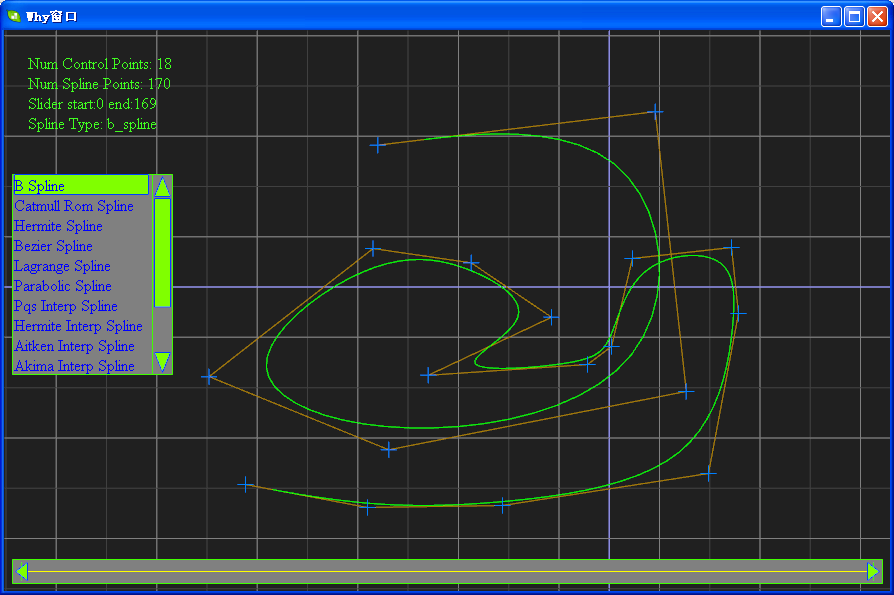
相关软件的下载地址为：http://files.cnblogs.com/WhyEngine/TestSpline.zip

最后要注意的是：B样条曲线不会经过其控制点。靠，我一直以为是经过的。因为B样条是我唯一在项目中使用过的。我用它来平滑游戏中角色刀光所划出的曲面，不过这种细节也没必要再去修改了。