题解 P5239 【回忆京都】

你们这些写题解的，就不能把话说清楚嘛！（吐槽1）

你们这些出题的，就不能多出点东方嘛！（吐槽2）

你们这些做题的，就不来写一篇详细一点的题解嘛！（吐槽3）

以上均是个人吐槽，纯属吐槽，不带任何针对性和感情色彩。

---

声明：

本题解适宜蒟蒻（比如我等）观看，若卡关，可以来此题解领提示。

小金羊写的题解致力于让刚刚学习二维数组的同学都能明白！！

把我顶上去让像我一样的juruo明白一下

---

回到正题。

首先还是看看这个题咋推出来的和杨辉三角&二位前缀和有关系？

我自己用python 3先手推了一下组合数，

先上python 3推组合数的代码:

import os
def jc(num):
  if num is 0 or num is 1:
   return 1
  else :
  return num*jc(num-1)
#阶乘递归版，适用于自己造的小型数据
#不是机惨w......
def zhs(i,j):
  if i > j :
    return 0
  else :
    return jc(j)/(jc(i)*jc(j-i))
#组合数配合阶乘递归，适用于小型数据推算

n=int(input())
while n is not 0:
  n-=1
  L=list(input().split())
  print(zhs(int(L[0]),int(L[1])))
  os.system("pause")
'''
print("Exit?",end=' ')
if input() is 'Yes':exit(1)
else :exit(1)
'''

一个个试一下，然后就发现这样一个鬼畜事件：



打眼一看：好像跟杨辉三角有那么点联系......

哦！缺了第一列的杨辉三角！

然后杨辉三角创造方法:\(O(1000^2\div 2)\)递推打表!

公式：

\[yh[i][j]=yh[i-1][j-1]+yh[i-1][j]
\]

别忘了取模(废话)

---

等等......

这个和此题有什么联系吗？

这个题让求组合数的和。

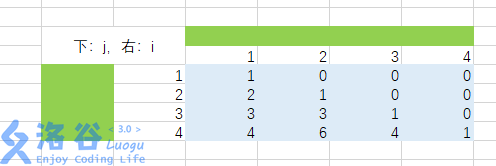
求和，先把区间用yellow色画出来。

然后发现......

(下图中填充黄色的是求和区域，紫色是和)

你发现了吗？这是一个二重的杨辉三角！

其实就是一个二维的前缀和预处理工作。

没有事情干的同学，树状数组&线段树都可解决这个问题。

根本就是两次递推打表!

然后这个题第一次我竟然只有10分......

---

但是要追求一个最优的方法。

这个时候我们要改一下原先的变量定义，是关于ans[i][j]方面:

设ans[i][j]表示的是前i列前j行的前缀和。

推出这个题前缀和公式的过程：

杨辉三角到底有什么好处？

其实杨辉三角给你预处理了单列上的前缀和。

然后单列上前缀和用汉语表示就是：

杨辉三角形第i列上前j行の前缀和就是杨辉三角形第i+1行第j+1列上的数据。

数学公式？（第一个中括号内暂定是1）

\[ans[1][j]=yh[1+1][j+1]
\]

根据以上推论，得出很多列的（就是二维的）前缀和推论。

汉语表达：

前i+1列前j+1行的前缀和就等于前i+1列前j行的前缀和加上前i+1列第j+1行的前缀和（即杨辉三角形第i+2行第j+2列那一项）。

公式？

\[ans[i][j]=ans[i][j-1]+yh[i+1][j+1]
\]

这样避免了许多不必要的记公式过程......

Upd4 2019/3/6:

有同学问，为啥是给你预处理了单列上的前缀和？

我们根据\(yh[i][j]=yh[i-1][j-1]+yh[i-1][j]\)，

那么又\(\because yh[i-1][j]=yh[i-2][j-1]+yh[i-1][j]\)......

以此类推，得到yh[i+1][j+1]，相当于我们得到了杨辉三角第j列的前i个数的和+\(yh[1][j]\)。

且根据我们杨辉三角靠左排列放置的方式，\(yh[1][j](j>0)\)必定为0。（观察可知\(yh[0][0]\)的右侧即\(yh[0][1]=0\)，而右侧\(yh[0][1]\)和右侧数据都是0）

于是我们得出递推公式，ans[i][j]=ans[i][j-1]+yh[i+1][j+1]。

到这里，我们找到了一个非常完美的没有过多数据+-的操作。

（qwq比cz dalao的算法的常数小）

坑点：

1.你以为取了mod就不会爆负数吗？太天真啦！

\(\therefore ans=(ans+mod)\)%\(mod\)

2.你以为我会\(O(2\cdot 1000^2)\)做吗？太天真啦！

复杂度\(O(1000^2\div 2+1000^2+query)\)

---

Upd1 2019/3/3:

关于代码和蒟蒻的二维前缀和求法补充完善

代码来辣！

求前缀和还是预处理吧......线段树什么的玩不来......

注意下面代码，求前缀和的时候意义和求杨辉三角的时候有所不同。

（原因见上面）

#include <iostream>
#include <cstdio>
#include <map>

using namespace std;
typedef long long int lli;
const int maxn=1008;
const lli mod=19260817;
lli yh[maxn+1][maxn+1],ans[maxn+1][maxn+1];
int n,m,q;

void Init()
{
    for (register int i=0;i<=1004;i++)
    {
        yh[i][i]=1;
    }
    for (register int i=0;i<=1004;i++)
    {
        yh[i][0]=1;
    }
    for (register int i=2;i<=1004;i++)
    {
        for (register int j=1;j<=i;j++)
        {
            yh[i][j]=(yh[i-1][j-1]+yh[i-1][j]+mod)%mod;
        }
    }
    //杨辉三角形的生成方式
    for (register int i=1;i<=1004;i++)
    {//前i列
        for (register int j=1;j<=1004;j++)
        {//前j行
            ans[i][j]=(ans[i][j-1]+yh[i+1][j+1]+mod)%mod;
        }
    }
    //二维前缀和的生成方式
}
int main()
{
    Init();
    scanf("%d",&q);
    while (q--)
    {
        scanf("%d%d",&n,&m);
        printf("%lld\n",ans[m][n]);
        //注意ans[][]的定义！！
    }
    return 0;
}

Upd2 2019/3/3:

重新更正代码，实际4-WA，现在AC。

原因在于这个算法的局限性：

实际上需要推到1000+，时间复杂度上虽然小了，但是容易边界数据卡没了......

实际上我就是这样4-WA：read 0的......