Python科学计算系列11—几何绘图

1.显函数图像绘制

例：绘制y=sinx的图像

代码如下：

from sympy import *

x = symbols('x')
plot(sin(x), (x, -2 * pi, 2 * pi))

运行结果：

2.隐函数图像绘制

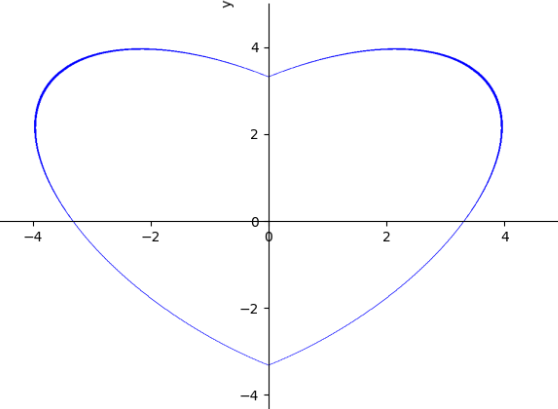
例：绘制11x²-12|x|y+11y²=121的图像

代码如下：

from sympy import *

x, y = symbols('x y')
plot_implicit(Eq(11 * x ** 2 - 12 * abs(x) * y + 11 * y ** 2, 121))

运行结果：

3.三维图像绘制

例：绘制y=xe^(-x²-y²)的图像

代码如下：

from sympy import *
from sympy.plotting import plot3d

x, y, z = symbols('x y z')
plot3d(x * exp(-x ** 2 - y ** 2), (x, -3, 3), (y, -2, 2))

运行结果：

4.三维爱心图像

代码如下：

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import matplotlib.pyplot as plt
import numpy as np

def heart_3d(x, y, z):
    return (x ** 2 + (9 / 4) * y ** 2 + z ** 2 - 1) ** 3 - x ** 2 * z ** 3 - (9 / 80) * y ** 2 * z ** 3

def plot_implicit(fn, bbox=(-1.5, 1.5)):
    xmin, xmax, ymin, ymax, zmin, zmax = bbox * 3
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    A = np.linspace(xmin, xmax, 100)
    B = np.linspace(xmin, xmax, 40)
    A1, A2 = np.meshgrid(A, A)

    for z in B:
        X, Y = A1, A2
        Z = fn(X, Y, z)
        cset = ax.contour(X, Y, Z + z, [z], zdir='z', colors=('r',))

    for y in B:
        X, Z = A1, A2
        Y = fn(X, y, Z)
        cset = ax.contour(X, Y + y, Z, [y], zdir='y', colors=('red',))

    for x in B:
        Y, Z = A1, A2
        X = fn(x, Y, Z)
        cset = ax.contour(X + x, Y, Z, [x], zdir='x', colors=('red',))
    ax.set_zlim3d(zmin, zmax)
    ax.set_xlim3d(xmin, xmax)
    ax.set_ylim3d(ymin, ymax)
    # 取消坐标轴显示
    plt.axis('off')
    plt.show()

if __name__ == '__main__':
    plot_implicit(heart_3d)

运行结果：