边缘检测及Canny算法

对边缘的直观理解

边缘有助于我们对图像进行语义理解。直观上，边缘发生在图像强度值变化剧烈的地方

如何描述变化？自然是用导数/梯度

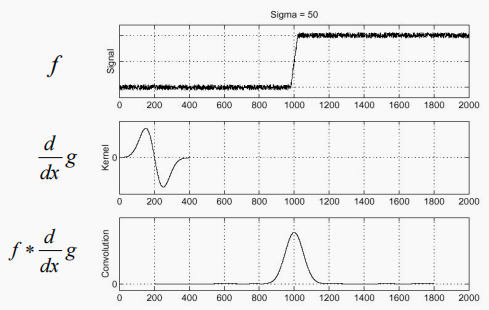
如上图，我们对图中的信号在水平方向上求导，可以得到右侧的导数图像，可以看到，它在边缘处由于信号发生剧烈变化，导数产生了极值。因此，导数的极值点能帮助我们定位边缘所在。

用卷积描述导数

对于一个二元的连续函数f(x,y)其偏导数可由如下极限得到：

\[\frac{\partial f(x, y)}{\partial x} = \lim_{\varepsilon \to 0} \frac{f(x + \varepsilon, y) - f(x, y)}{\varepsilon}
\]

而对于离散的图像数据，我们通常使用如下表达式近似偏导数，也就是有限差分的方式：

\[\frac{\partial f(x, y)}{\partial x} \approx \frac{f(x + 1, y) - f(x, y)}{1}
\]

而这种计算方式，可以用卷积核的形式进行处理：

x方向上的导数可理解为右边的像素减去我自己，转化成卷积核长这样：

y方向上的导数可理解为上面的像素减去我自己，转化成卷积核长这样：

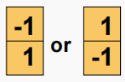
用这种卷积核对图像做卷积，得到每个像素点在x和y方向上的导数：

其他几种表示导数的卷积核

除了上面这种”极简“导数卷积核外，我们常用的还有以下几种卷积核：

Prewitt

该算子考虑了上下两层的信息，增强了对弱边缘的捕获能力，更具有鲁棒性。

Sobel

该算子在其中心列/行上权重为2，也就是说更关注自身所在列/行，能够抵御一定的噪声干扰。

这个卷积核可以分解为

\[\begin{bmatrix}
1 \\
2 \\
1
\end{bmatrix}
\cdot
\begin{bmatrix}
-1 & 0 & 1
\end{bmatrix}
\]

可以把卷积分解成两次小的卷积操作，降低计算复杂度。

Roberts

可以检测45°/135°边缘。

从工程实践来说，Sobel算子具有良好的抗噪性和运算效率，其综合性能最优，是最常用的求导卷积核。OpenCV等库的默认实现。为了解决其在方向上的局限性（x，y两个方向），也常组合使用多方向核（如8方向Sobel扩展）。

图像2D上的导数---梯度

1D上叫导数，2D上叫梯度。把函数对x和y的偏导数放到一个向量中，该向量就表示了梯度信息。

\[\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]
\]

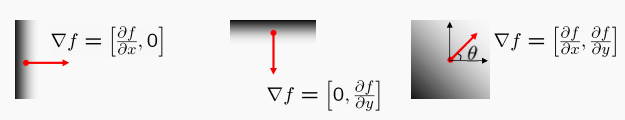
这个梯度向量的方向，就表达了当前像素点主要是在这个方向上变化

\[\theta = \tan^{-1} \left( \frac{\partial f}{\partial y} / \frac{\partial f}{\partial x} \right)
\]

向量的长度，就是在这个方向上变化的快慢

\[||\nabla f|| = \sqrt{\left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2}
\]

该点的梯度长度，决定了该点是不是边缘，边缘点的梯度变化大，非边缘的梯度小。

梯度的方向，垂直于边。

把梯度的模算出来，画在图像上，就得到了梯度强度图，取一个阈值，就能取到边缘上的点。

（也可以理解为取极值点，但极值点可能比较离散，连不成一条线）

真实场景的应用---高斯偏导核

对于实际图像来说，由于噪声存在，如果直接使用上面的导数卷积核，就会造成如下情况：

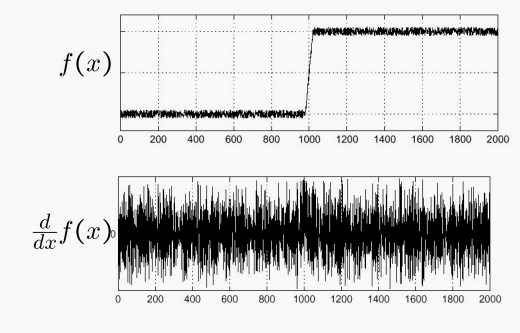
导数的极值到处都是。如何处理噪声？我们可以做高斯平滑。

如下图所示，我们先做平滑，再进行求导

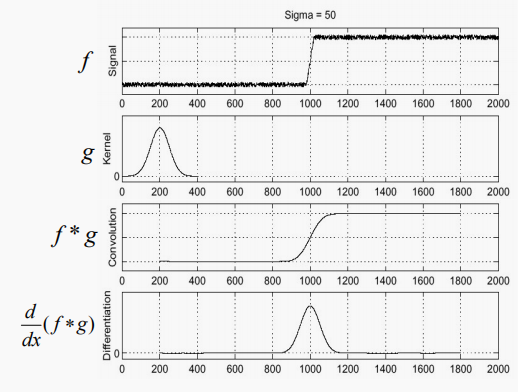
这两步又可以合成一步（卷积的交换律，结合律），也就是

\[\frac{d}{dx}(f*g) = f * \frac{d}{dx}g
\]

高斯平滑加导数，等效于直接对高斯核做导数，然后与之卷积

也就是高斯偏导核

二维的高斯偏导核图像如图：

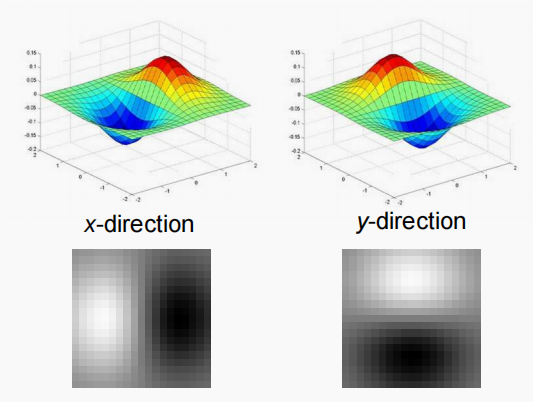
注意：这里的x方向的高斯偏导核是不可以再分解成两个高斯核的，可以从高斯函数公式的导数公式看出。

原高斯核可以分成两个方向的高斯核相乘。也就可以先对x方向求卷积，再对y方向求卷积。

高斯偏导核的σ影响：下图σ为1，3，7

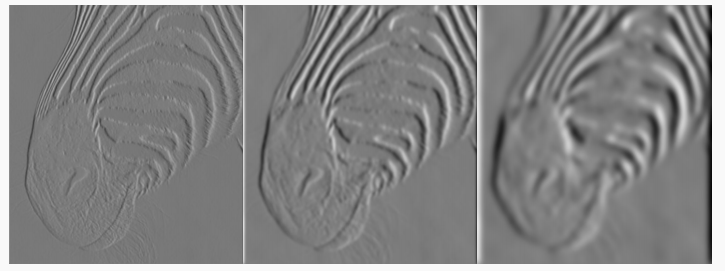
可以看到σ越小，检测到的边缘越精细，越大，检测到的边缘的尺度越大。

高斯核 vs 高斯偏导核

高斯核：

• 高频率波，低通滤波
• 权值为正
• 加权和为正

高斯偏导核

• 高斯核的导数
• 可为负
• 加权和为0
• 高对比度（边缘）处有高绝对值的加权值

Canny算法

通过上文中的方法，我们首先计算高斯偏导核的卷积结果，得到梯度模的图像

设置阈值对边缘点进行筛选：

这里存在一个问题：由于做了高斯模糊，阈值以上部分边缘看起来很粗

如上图，我们设置阈值之后，阈值以上的部分是一段相对较粗的区域，边缘的具体位置不精确。而实际上我们更期望得到的边缘是更精准的一条线。这里我们需要引入非最大化抑制的方法。

非最大化抑制 non-maximun suppression

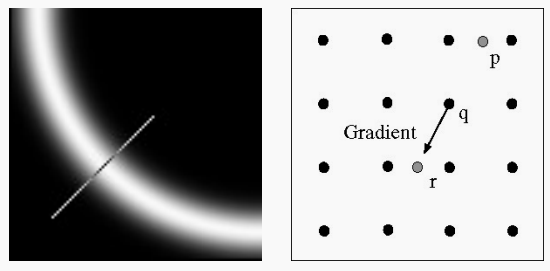
我们在每个像素的梯度方向上判断前后两个点和自身模的大小，如果自己是最大的则保留，否则不保留。

如上图所示，q点的梯度方向上，前后两个点分别是r和p，梯度大小可以通过像素点上的梯度插值得到。判断p、q、r的梯度大小，如果q是最大的，则q点保留下来；如果q不是最大的，则q点舍弃。

由于梯度方向和边缘是垂直关系，这样从整体来看，我们最终留下了那个边缘垂线方向上的极值点。

然而这里又产生了新问题：求得结果不连通

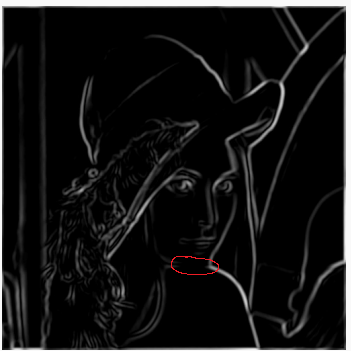
如图中人脸下巴位置处，理应有一条边缘连接起来，而由于光照等因素影响，使得该处梯度变化不明显，检测出的边缘无法连通；而如果我们降低阈值，有可能引入更多的噪声因素。

此时，我们可以引入双阈值检测方法。

双阈值检测 Hysteresis Thresholding

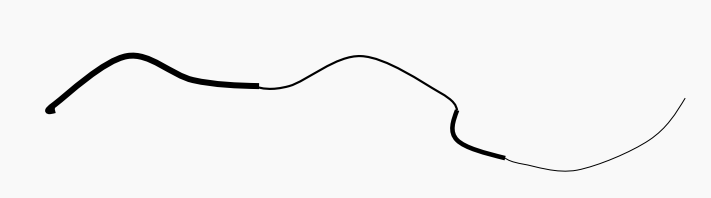
该方法的核心思路在于设置高低两种阈值，筛选出可信的边缘，再利用边缘的连通性补全弱边缘信息。

1. 用高阈值检测出图中粗的部分，这部分梯度变化剧烈且稳定，受噪声干扰小，比较鲁棒。
2. 用低阈值检测弱边缘，这部分可能包含较多的候选点，也包含更多的噪声。
3. 这里引入一个先验条件，有效的弱边缘一定与高阈值检测出的强边缘连通。因此，我们可以检查弱边缘像素候选点的8邻域像素：
   • 若邻域内存在强边缘像素，则该弱边缘点标记为有效
   • 若邻域内不存在强边缘像素，则该弱边缘点视为噪声，舍弃掉。
     
     下图为通过双阈值检测得到的结果：
     
     

总结Canny算法步骤

1. ​使用高斯导数过滤图像
   
   首先，对图像进行高斯滤波，以减少噪声并平滑图像，为后续的边缘检测做好准备。

2. ​找到梯度的大小和方向
   
   计算图像的梯度，确定每个像素点的梯度幅度和方向。梯度幅度表示边缘的强度，梯度方向表示边缘的方向。

3. ​非最大抑制（Non-maximum suppression）​
   
   将宽的“脊”缩小到单个像素宽度。通过比较每个像素点的梯度幅度与其相邻像素点，保留局部最大值，从而细化边缘。

4. ​双阈值检测​
   
   定义高低两个阈值：

   • 使用高阈值初步检测边缘曲线，确保鲁棒性强的边缘被保留。
   • 使用低阈值来链接边缘曲线，把和强边缘相接的弱边缘连接起来。