kafka 消费模型图
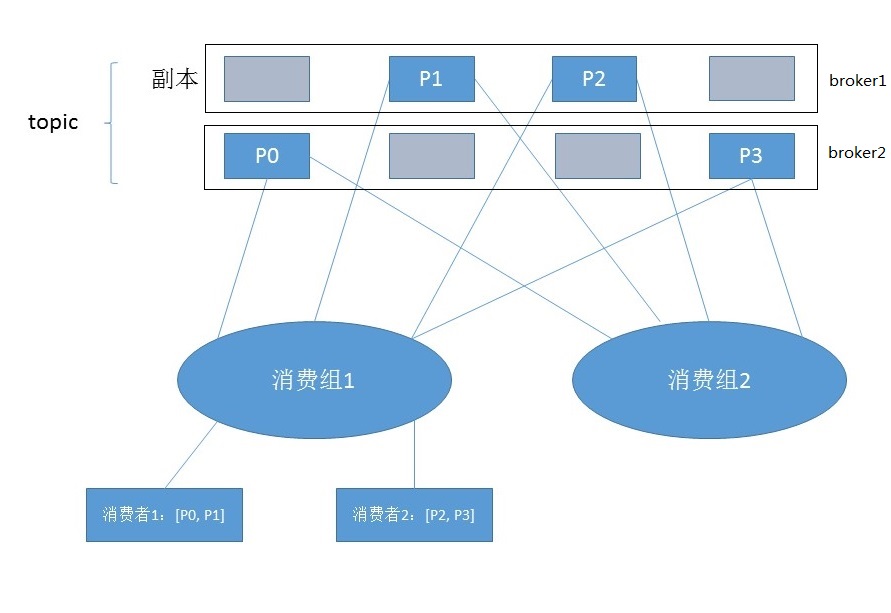
kafka 消费模型图的更多相关文章
- kafka 消费
前置资料 kafka kafka消费中的问题及解决方法: 情况1: 问题:脚本读取kafka 数据,写入到数据库,有时候出现MySQL server has gone away,导致脚本死掉.再次启 ...
- kafka架构,消息存储和生成消费模型,Kafka与其他队列对比,零拷贝,Kafka基本介绍
kafka架构,消息存储和生成消费模型,Kafka与其他队列对比,零拷贝,Kafka基本介绍 一.初识kafka 1.1SparkStreaming+Kafka好处: 1.2Kafka的架构: 二.k ...
- 分享一些 Kafka 消费数据的小经验
前言 之前写过一篇<从源码分析如何优雅的使用 Kafka 生产者> ,有生产者自然也就有消费者. 建议对 Kakfa 还比较陌生的朋友可以先看看. 就我的使用经验来说,大部分情况都是处于数 ...
- Kafka设计解析(十三)Kafka消费组(consumer group)
转载自 huxihx,原文链接 Kafka消费组(consumer group) 一直以来都想写一点关于kafka consumer的东西,特别是关于新版consumer的中文资料很少.最近Kafka ...
- 涨姿势了解一下Kafka消费位移可好?
摘要:Kafka中的位移是个极其重要的概念,因为数据一致性.准确性是一个很重要的语义,我们都不希望消息重复消费或者丢失.而位移就是控制消费进度的大佬.本文就详细聊聊kafka消费位移的那些事,包括: ...
- RabbitMQ,RocketMQ,Kafka 消息模型对比分析
消息模型 消息队列的演进 消息队列模型 发布订阅模型 RabbitMQ的消息模型 交换器的类型 direct topic fanout headers Kafka的消息模型 RocketMQ的消息模型 ...
- kafka消费
消费模型 kafka模型使用了 发布/订阅.点对点模型. 消息发布 在producer端,通过分片策略,找到对应topic下面的Partition leader,把消息发送到当前Partition 消 ...
- UML动态模型图简单介绍
UML动态模型图描述了系统动态行为的各个方面,包括用例图.序列图.协作图.活动图和状态图.下面就每种图做一个简单介绍: 用例图 用例图描述系统外部的执行者与系统提供的用例之间的某种联系.所谓用例是指对 ...
- Go语言学习之12 etcd、contex、kafka消费实例、logagent
本节内容: 1. etcd介绍与使用 2. ElastcSearch介绍与使用 1. etcd介绍与使用 概念:高可用的分布式key-value存储,可以使用配置共享和服务发现 ...
随机推荐
- (Review cs231n) CNN in Practice
Make the most of your data Data augmentation 加载图像后,对图像做一些变化,这些变换不改变图像的标签. 通过各种变换人为的增大数据集,可以避免过拟合提高模型 ...
- dynamic的使用
一.在没有dynamic之前,我们想要获取返回object对象里的属性的值时,使用反射的方法来获取该对象的属性值. class Program { static void Main(string[] ...
- vue 路由守卫
router.beforeEach((to, from, next) => { const nextRoute = [ 'login']; var token = window.localSto ...
- JS,JQuery小知识
http://blog.163.com/wumingli456@126/blog/static/28896414201112252456459/?suggestedreading&wumii
- Git_GitHub-使用过程遇到的问题——坑(持续添加)
push错误——>master git push -u origin master 最后找到解决办法如下: 1.先删除远程 Git 仓库 $ git remote rm origin 2.再添加 ...
- jenkins 构建nodejs-pipeline流水风格的任务
Step3 上图代码如下 node("master"){ //warp([$class:'BuildUser']) {BUILD_USER = BUILD_USER} GIT_NA ...
- sql 中 and 和 or的坑
请参考以下链接 https://blog.csdn.net/u011064736/article/details/70257366
- nodejs-使用multer实现多张图片上传,express搭建脚手架
nodejs-使用multer实现多张图片上传,express搭建脚手架 在工作中,我们经常会看到用户有多张图片上传,并且预览展示的需求.那么在具体实现中又该怎么做呢? 本实例需要nodejs基础,本 ...
- JS(JavaScript)的初了解7(更新中···)
1.逻辑运算 || && ! 1||2 5&&4 !0 || 遇到第一个为true的数字就终止并返回 && 遇到第一个为false的值 就终 ...
- 错误模块“AspNetCoreModuleV2"解决
如图 HTTP 错误 500.21 - Internal Server Error 处理程序"aspNetCore"在其模块列表中有一个错误模块"AspNetCoreMo ...
