Appium+python自动化15-在Mac上环境搭建

前言

mac上搭建appium+python的环境还是有点复杂的，需要准备的软件

1.nodejs

2.npm

3.cnpm

4.appium

5.pip

6.Appium-Python-Client

一、nodejs安装

1.nodejs下载地址：https://nodejs.org/

2.下载完成后傻瓜式下一步安装

3.打开终端，查看版本号是否安装成功，输入：node -v

二、npm安装

1.打开终端，输入：sudo bash

2.继续输入：sudo curl -L https://npmjs.org/install.sh | sh

3.看到上图所示，就是安装完成了。检查npm是否安装成功，先关掉终端，再重新打开，输入：npm -v

三、cnpm安装

1.用npm安装appium时候，中途会报错(由于某种原因,直接用npm下载安装会有好多网络问题，安装淘宝的cnpm要比npm好用),

所以这里用cnpm代替了npm

2.打开终端，输入sudo npm install -g cnpm --registry=https://registry.npm.taobao.org

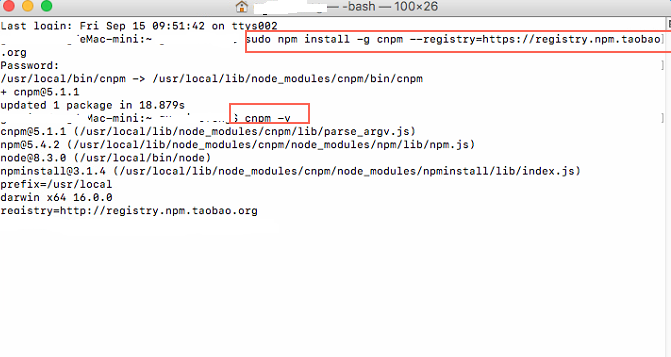
四、appium安装

1.appium的安装有两种：一种是有GUI图形界面的，下载dmg包，手动安装；另外一种是通过cnpm指令安装的，无图形界面

方式一：下载dmg包手动安装（新手推荐）

官方下载地址：http://appium.io/

百度云下载地址：链接: https://pan.baidu.com/s/1pKAj1qj 密码: q3qu

下载后傻瓜式下一步安装就行了

方法二：cnpm安装（无图形界面）

2.这里下载1.6.3的版本，@后面可以指定版本号。终端输入：cnpm install -g appium@1.6.3

（要是报错，就用sudo去安装：sudo cnpm install -g appium@1.6.3）

3.安装完成后，想启动appium，就在终端输入:appium

看到如下界面：Welcome to Appium v1.6.3说明安装成功了

----------------------以上是安装appium相关包，接下来是准备python相关的包---------------

五、pip安装

1.pip是安装python第三方包的最主要的一个小工具，打开终端输入：sudo easy_install pip

六、Appium-Python-Client

1.安装appium的python包，打开终端输入：sudo pip install Appium-Python-Client

2.中途要是弹出Password的提示，就输入当前用户的密码就行

还需要安装的软件：

1.jdk

2.xcode

3.pycharm

在学习过程中有遇到疑问的，可以appium+python QQ群交流:330467341