代码随想录Day16

513.找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

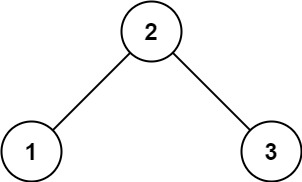
输入: root = [2,1,3]
输出: 1

示例 2:

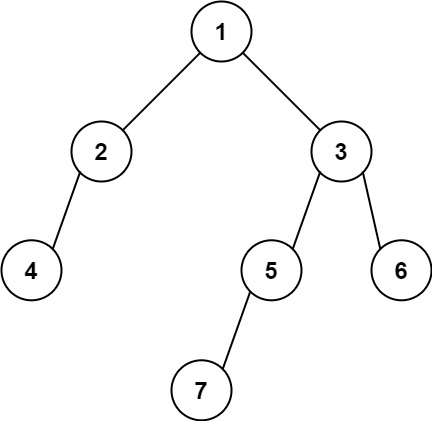
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示:

二叉树的节点个数的范围是 [1,10⁴]

-2³¹ <= Node.val <= 2³¹ - 1

---

正解

我们来分析一下题目：在树的最后一行找到最左边的值。

首先要是最后一行，然后是最左边的值。

如果使用递归法，如何判断是最后一行呢，其实就是深度最大的叶子节点一定是最后一行。

所以要找深度最大的叶子节点。

那么如何找最左边的呢？可以使用前序遍历，保证优先左边搜索；

然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。

1. 确定递归函数的参数和返回值
   
   参数必须有要遍历的树的根节点，还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了，所以递归函数的返回类型为void。
   
   本题还需要类里的两个全局变量，maxLen用来记录最大深度，result记录最大深度最左节点的数值。
2. 确定终止条件
   
   当遇到叶子节点的时候，就需要统计一下最大的深度了，所以需要遇到叶子节点来更新最大深度。
3. 确定单层递归的逻辑
   
   在找最大深度的时候，递归的过程中依然要使用回溯。

上代码(●'◡'●)

class Solution {
public:
    int maxDepth = INT_MIN;
    int result;
    void traversal(TreeNode* root, int depth) {
        if (root->left == NULL && root->right == NULL) {
            if (depth > maxDepth) {
                maxDepth = depth;
                result = root->val;
            }
            return;
        }
        if (root->left) {
            traversal(root->left, depth + 1); // 隐藏着回溯
        }
        if (root->right) {
            traversal(root->right, depth + 1); // 隐藏着回溯
        }
        return;
    }
    int findBottomLeftValue(TreeNode* root) {
        traversal(root, 0);
        return result;
    }
};

112.路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

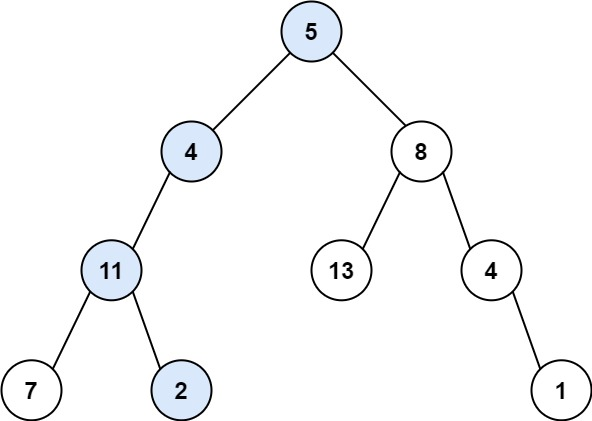
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

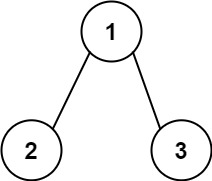
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内

-1000 <= Node.val <= 1000

-1000 <= targetSum <= 1000

---

正解

可以使用深度优先遍历的方式（本题前中后序都可以，无所谓，因为中节点也没有处理逻辑）来遍历二叉树。

1. 确定递归函数的参数和返回类型
   
   参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。
   
   返回值：遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。
2. 确定终止条件
   
   首先计数器如何统计这一条路径的和呢？
   
   不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。
   
   如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。
   
   如果遍历到了叶子节点，count不为0，就是没找到。
3. 确定单层递归的逻辑
   
   因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。
   
   递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。

上代码(●'◡'●)

class Solution {
public:
    bool hasPathSum(TreeNode* root, int sum) {
        if (!root) return false;
        if (!root->left && !root->right && sum == root->val) {
            return true;
        }
        return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
    }
};

可以看出，代码很精简，但隐藏了许多过程，包括回溯的过程；

如果都展开的话应该是这个样子：

class Solution {
private:
    bool traversal(TreeNode* cur, int count) {
        if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
        if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回

        if (cur->left) { // 左
            count -= cur->left->val; // 递归，处理节点;
            if (traversal(cur->left, count)) return true;
            count += cur->left->val; // 回溯，撤销处理结果
        }
        if (cur->right) { // 右
            count -= cur->right->val; // 递归，处理节点;
            if (traversal(cur->right, count)) return true;
            count += cur->right->val; // 回溯，撤销处理结果
        }
        return false;
    }

public:
    bool hasPathSum(TreeNode* root, int sum) {
        if (root == NULL) return false;
        return traversal(root, sum - root->val);
    }
};

106.从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

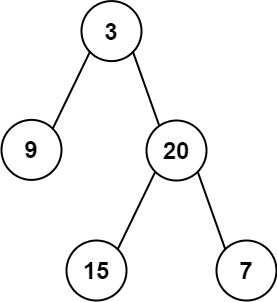
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000

postorder.length == inorder.length

-3000 <= inorder[i], postorder[i] <= 3000

inorder 和 postorder 都由 不同 的值组成

postorder 中每一个值都在 inorder 中

inorder 保证是树的中序遍历

postorder 保证是树的后序遍历

---

正解

首先回忆一下如何根据两个顺序构造一个唯一的二叉树：

以 后序数组的最后一个元素为切割点，先切中序数组；

根据中序数组，反过来再切后序数组。

一层一层切下去，每次后序数组最后一个元素就是节点元素。



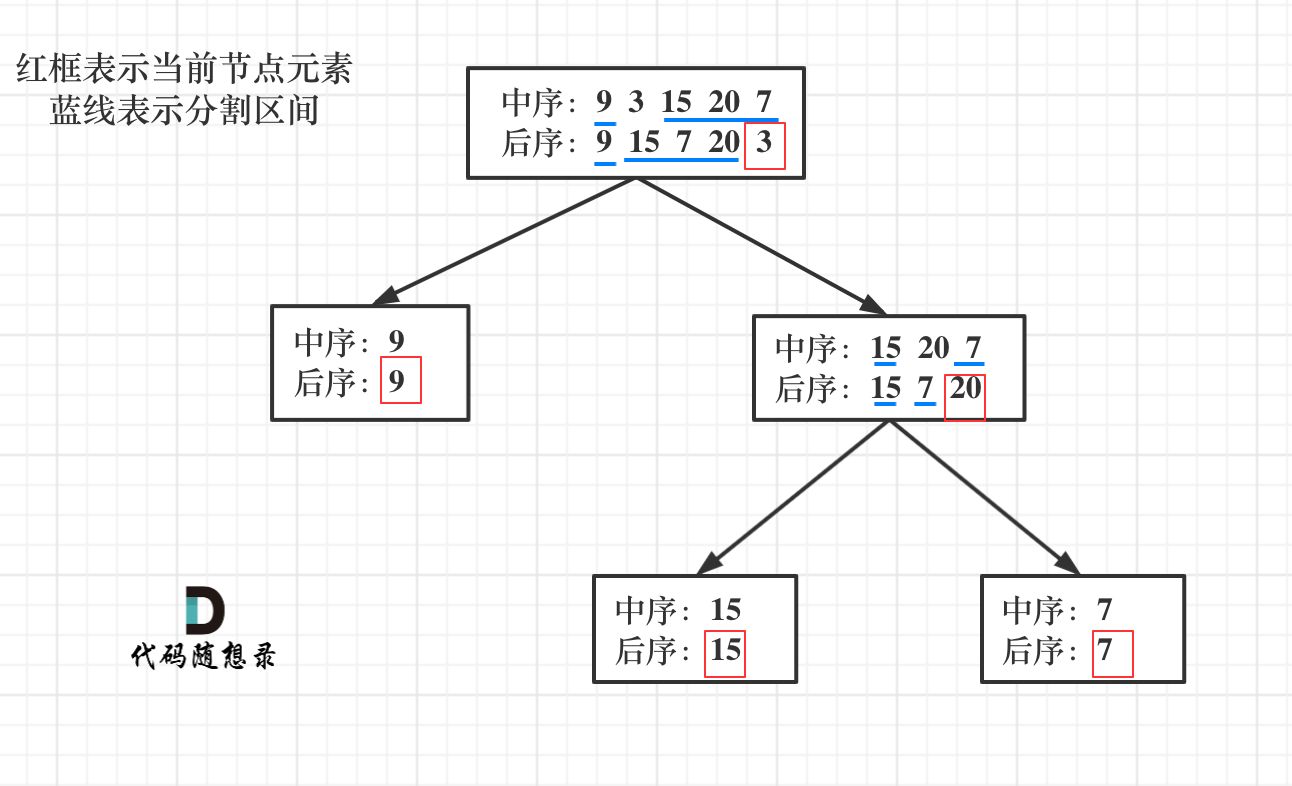
说到一层一层切割，就应该想到了递归。

来看一下一共分几步：

• 第一步：如果数组大小为零的话，说明是空节点了。

• 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。

• 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

• 第四步：切割中序数组，切成中序左数组和中序右数组 （注意顺序，一定是先切中序数组）

• 第五步：切割后序数组，切成后序左数组和后序右数组

• 第六步：递归处理左区间和右区间

此时应该注意确定切割的标准，是左闭右开，还有左开右闭，还是左闭右闭；

这个就是不变量，要在递归中保持这个不变量。

在切割的过程中会产生四个区间，把握不好不变量的话，一会左闭右开，一会左闭右闭，必然乱套！

首先要切割中序数组，为什么先切割中序数组呢？

切割点在后序数组的最后一个元素，就是用这个元素来切割中序数组的，所以必要先切割中序数组。

中序数组相对比较好切，找到切割点（后序数组的最后一个元素）在中序数组的位置，然后切割

接下来就要切割后序数组了。

首先后序数组的最后一个元素指定不能要了，这是切割点 也是 当前二叉树中间节点的元素，已经用了。

后序数组的切割点怎么找？

后序数组没有明确的切割元素来进行左右切割，不像中序数组有明确的切割点，切割点左右分开就可以了。

此时有一个很重的点，就是中序数组大小一定是和后序数组的大小相同的（这是必然）

中序数组我们都切成了左中序数组和右中序数组了；

那么后序数组就可以按照左中序数组的大小来切割，切成左后序数组和右后序数组。

此时，中序数组切成了左中序数组和右中序数组，后序数组切割成左后序数组和右后序数组。

接下来可以递归了。

上代码(●'◡'●)

class Solution {
private:
    TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
        if (postorder.size() == 0) return NULL;

        // 后序遍历数组最后一个元素，就是当前的中间节点
        int rootValue = postorder[postorder.size() - 1];
        TreeNode* root = new TreeNode(rootValue);

        // 叶子节点
        if (postorder.size() == 1) return root;

        // 找到中序遍历的切割点
        int delimiterIndex;
        for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }

        // 切割中序数组
        // 左闭右开区间：[0, delimiterIndex)
        vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
        // [delimiterIndex + 1, end)
        vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );

        // postorder 舍弃末尾元素
        postorder.resize(postorder.size() - 1);

        // 切割后序数组
        // 依然左闭右开，注意这里使用了左中序数组大小作为切割点
        // [0, leftInorder.size)
        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
        // [leftInorder.size(), end)
        vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

        root->left = traversal(leftInorder, leftPostorder);
        root->right = traversal(rightInorder, rightPostorder);

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        return traversal(inorder, postorder);
    }
};

写博不易，请大佬点赞支持一下8~