协方差及matlib绘制

转自http://www.cnblogs.com/chaosimple/p/3182157.html

一、统计学的基本概念

统计学里最基本的概念就是样本的均值、方差、标准差。首先，我们给定一个含有n个样本的集合，下面给出这些概念的公式描述：

均值：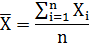

标准差：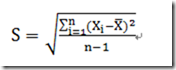

方差：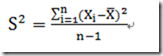

均值描述的是样本集合的中间点，它告诉我们的信息是有限的，而标准差给我们描述的是样本集合的各个样本点到均值的距离之平均。

以这两个集合为例，[0, 8, 12, 20]和[8, 9, 11, 12]，两个集合的均值都是10，但显然两个集合的差别是很大的，计算两者的标准差，前者是8.3后者是1.8，显然后者较为集中，故其标准差小一些，标准差描述的就是这种“散布度”。之所以除以n-1而不是n，是因为这样能使我们以较小的样本集更好地逼近总体的标准差，即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。

二、为什么需要协方差

标准差和方差一般是用来描述一维数据的，但现实生活中我们常常会遇到含有多维数据的数据集，最简单的是大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集，我们当然可以按照每一维独立的计算其方差，但是通常我们还想了解更多，比如，一个男孩子的猥琐程度跟他受女孩子的欢迎程度是否存在一些联系。协方差就是这样一种用来度量两个随机变量关系的统计量，我们可以仿照方差的定义：

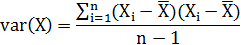
来度量各个维度偏离其均值的程度，协方差可以这样来定义：

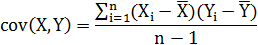
协方差的结果有什么意义呢？如果结果为正值，则说明两者是正相关的（从协方差可以引出“相关系数”的定义），也就是说一个人越猥琐越受女孩欢迎。如果结果为负值， 就说明两者是负相关，越猥琐女孩子越讨厌。如果为0，则两者之间没有关系，猥琐不猥琐和女孩子喜不喜欢之间没有关联，就是统计上说的“相互独立”。

从协方差的定义上我们也可以看出一些显而易见的性质，如：

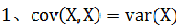
三、协方差矩阵

前面提到的猥琐和受欢迎的问题是典型的二维问题，而协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算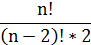个协方差，那自然而然我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

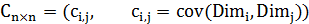
这个定义还是很容易理解的，我们可以举一个三维的例子，假设数据集有三个维度，则协方差矩阵为：

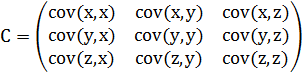
可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度的方差。

四、Matlab协方差实战

必须要明确一点，协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。以下的演示将使用Matlab，为了说明计算原理，不直接调用Matlab的cov函数：

首先，随机生成一个10*3维的整数矩阵作为样本集，10为样本的个数，3为样本的维数。

图 1 使用Matlab生成样本集

根据公式，计算协方差需要计算均值，前面特别强调了，协方差矩阵是计算不同维度之间的协方差，要时刻牢记这一点。样本矩阵的每行是一个样本，每列是一个维度，因此我们要按列计算均值。为了描述方便，我们先将三个维度的数据分别赋值：

图 2 将三个维度的数据分别赋值

计算dim1与dim2，dim1与dim3，dim2与dim3的协方差：

图 3 计算三个协方差

协方差矩阵的对角线上的元素就是各个维度的方差，下面我们依次计算这些方差：

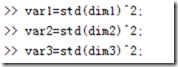
图 4 计算对角线上的方差

这样，我们就得到了计算协方差矩阵所需要的所有数据，可以调用Matlab的cov函数直接得到协方差矩阵：

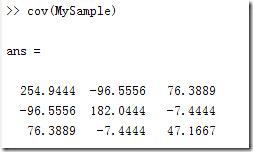
图 5 使用Matlab的cov函数直接计算样本的协方差矩阵

计算的结果，和之前的数据填入矩阵后的结果完全相同。

五、总结

理解协方差矩阵的关键就在于牢记它的计算是不同维度之间的协方差，而不是不同样本之间。拿到一个样本矩阵，最先要明确的就是一行是一个样本还是一个维度，心中明确整个计算过程就会顺流而下，这么一来就不会迷茫了。

概率论的其他知识点：概率论中常用的公式 ：http://www.cnblogs.com/cv-pr/p/5182388.html

常见概率分布：http://blog.csdn.net/pipisorry/article/details/39076957

http://blog.csdn.net/pipisorry/article/details/49516209