纪中5日T3 1566. 幸运锁(lucky.pas/c/cpp)

1566. 幸运锁(lucky.pas/c/cpp)

题目描述

有一把幸运锁，打开它将会给你带来好运，但开锁时需要输入一个正整数（没有前导0）。幸运锁有一种运算，对于一个正整数，返回他的相邻两位数字间的差，如1135，运算结果为22(会去掉前导0)。
现在已知只有经过反复运算最终结果为7的数才能打开这把锁，给你一个区间[a,b]，问该区间中有多少个能打开幸运锁的幸运数。

输入

第一行两个整数a，b。

输出

一个整数K，表示共有多少个这样的数。

样例输入

1 10

样例输出

1

数据范围限制

【限制】

1<=a<=b<=10^9。

30%的数据有b<=10^6。

Solution（28分）

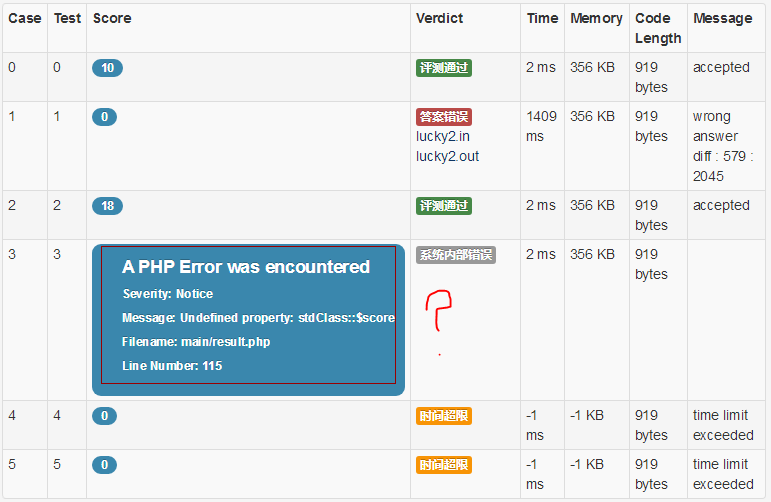
貌似正好遇上服务器出问题了呢

这就不是我的问题了

（这也不是服务器的问题嘛！你怎么可以这样想呢？）

我觉得我的代码是正确的

而测试点2呢，我用一个打表的程序也过了

table

首先奉上我的table.cpp

//幸运锁表
#include<bits/stdc++.h>
using namespace std;
int n,m,a,b,lucky,h,f[],ans;
int logn(int num)
{
    if(num==) return ;
    return log(num)/;
}
void fj(int num)
{
    int len=logn(num);
    for(int i=;i<len;i++)
    {
        f[i]=((int)(num/pow(,i)))%;
    }
    return;
}
void run(int num[],int len)
{
//    检测是否为0000000..7||0000000..*
    bool flag7=;
    for(int i=;i<len;i++)
    if(num[i]!=) {
        flag7=;
        break;
    }

    if(flag7)
    {
        if(num[]==)
        {
            cout<<h<<",";
            ans++;
        }

        return;
    }

//    算差
    int w[len];
    memset(w,,sizeof(w));
    for(int i=;i<len-;i++)
        w[i]=abs(num[i]-num[i+]);
//    删除前导零
    int flag0=;
    for(int i=len-;i>=;i--)
    {
        if(flag0)
        {
            if(num[i]==)
                len--;
            else
                flag0=;
        }
        else
            break;
    }
    run(w,len-);
}
int main()
{
//    freopen("lucky.in","r",stdin);
//    freopen("lucky表.txt","w",stdout);
    for(h=;h<=;h++)
    {
        //分解数字
        fj(h);
        run(f,logn(h));
    }
    cout<<"\nans="<<ans;
    return ;
}

想要过程解释，还请看注释。

正解会再做详细解释。

这个cpp可以打出从a~b所有满足条件的数

但我并没有找到什么规律鸭

Code（46分）

//幸运锁
#include<bits/stdc++.h>
using namespace std;
int n,m,a,b,lucky,f[],ans;
int logn(int num)
{
    if(num==) return ;//本来log(1)会等于0的
    return log(num)/;
}
void fj(int num)
{
    int len=logn(num);
    for(int i=;i<len;i++)
    {
        f[i]=((int)(num/pow(,i)))%;
    }
    return;
}
void run(int num[],int len)
{
//    检测是否为0000000..7||0000000..*
    bool flag7=;
    for(int i=;i<len;i++)
    if(num[i]!=) {
        flag7=;
        break;
    }
    //如果flag7==1，就说明该数只有个位了，其他位全是零
    if(flag7)
    {
        if(num[]==)
            ans++;
        return;//一个位数是一定不能变成7的
    }
//    算差
    int w[len];
    memset(w,,sizeof(w));//开始时忘了初始化，坑了我好久
    for(int i=;i<len-;i++)
        w[i]=abs(num[i]-num[i+]);//相邻两数之差要取绝对值
//    删除前导零
    int flag0=;
    for(int i=len-;i>=;i--)
    {
        if(flag0)
        {
            if(num[i]==)
                len--;
            else
                flag0=;
        }
        else
            break;

    }
    run(w,len-);//就是这里！ 求差后，len一定会自然的少一个
}
int main()
{
//    freopen("lucky.in","r",stdin);
//    freopen("lucky.out","w",stdout);
    cin>>a>>b;
    for(int i=a;i<=b;i++)
    {
        //分解数字
        fj(i);
        run(f,logn(i));
    }
    cout<<ans;

    return ;
}

修改了这个地方后，成功的又对了一个测试点。

下载一个数据看看？

File Not Found!

额

老师呢，看了看那些100分的同学的代码。

大小都是几MB几MB的。

又因为我是时间超限……

你明白了吗？

打表！

那个。。。源代码太长，我我我上传不了。

就先发个压缩包吧

https://files-cdn.cnblogs.com/files/send-off-a-friend/lucky.rar

数论

等待着数论的方法出现。。。

老师加油！