斯坦福机器学习视频笔记 Week1 Linear Regression and Gradient Descent

最近开始学习Coursera上的斯坦福机器学习视频，我是刚刚接触机器学习，对此比较感兴趣；准备将我的学习笔记写下来，

作为我每天学习的签到吧，也希望和各位朋友交流学习。

这一系列的博客，我会不定期的更新，希望大家多多批评指正。

Supervised Learning（监督学习）

在监督学习中，我们的数据集包括了算法的输出结果，比如具体的类别(分类问题)或数值（回归问题），输入和输出存在某种对应关系。

监督学习大致可分为回归（classification）和分类（regression）。

回归：对于连续型数值的预测；

分类：对于离散输出的预测，输出为某些具体的类别；

Unsupervised Learning（无监督学习）

在无监督学习中，我们对于输出的结果一无所知，根据数据的内在结构将数据聚类，我们无法得到预测结果的反馈。

总结：监督学习和无监督学习的重要区别，数据集的输出结果是否事先知道。

课程pdf：https://www.coursera.org/learn/machine-learning/supplement/d5Pt1/lecture-slides

Model Representation（模型表示）

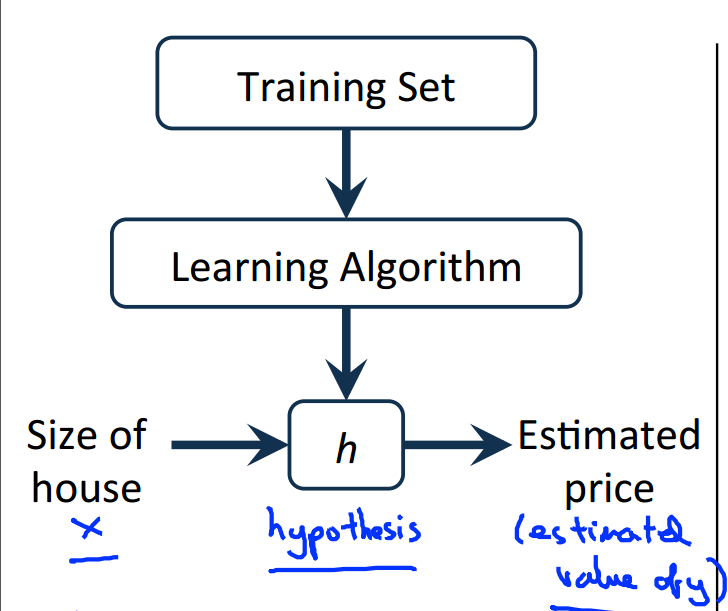
以上是监督学习问题的图示描述，我们的目标是，给定训练集，学习函数h：X→Y，使得h（x）是对于y有较好的预测值。

h（x）代表的是一个假设集合（Hypothesis ），我们要做的就是从这个假设集合中找出预测效果最好的那一个假设。

下面是后文将用到的符号表示，请务必明白其表示的意思，这个不难。

Cost Function（损失函数）

之前举的例子，关于房价的预测问题，是一个单变量的回归问题，输入数据只有x维度为1，

我们建立的模型是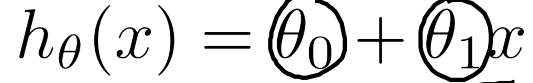，我们的目标是让这个直线尽可能的拟合所有数据，

即从数据的中心穿过，让我们的每个预测值h（x）与我们的已知数值y尽可能的接近。

那么，我们应该怎么选择最好的模型呢？通过求解参数theta1和theta2.

我们可以通过使用 cost function(损失函数)来测量我们的假设的准确性。 这需要使用来自x的输入

和实际输出y的假设的所有结果的平均差（实际上是平均值的更好的版本），如下。

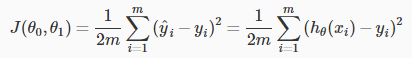
说明：其实损失函数 J 计算的是h（x）与真实值y之间的垂直距离的平方和均值。

关于为什么多一个1/2的问题，是为了以后求导方便，不用太在意这个。

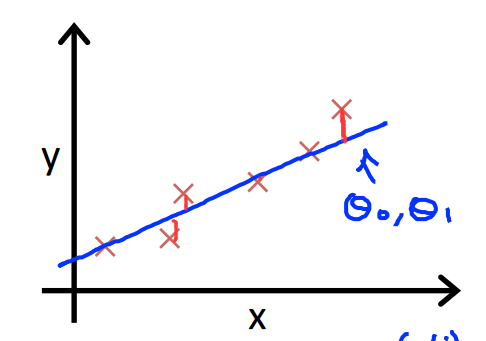
为了问题描述的方便，首先使用上图右边的简单模型，只有一个参数theta1.

下图是对数据样本点”X“的拟合状态，

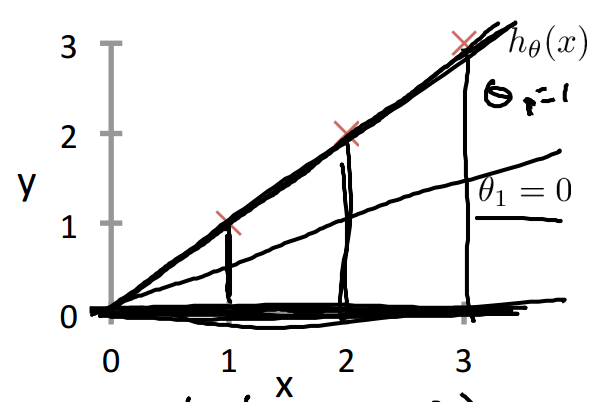
当在上图中我们随意旋转h（x），将会得到不同的 J 值，可以得到下面的关于theta1 损失函数 J 的图像：

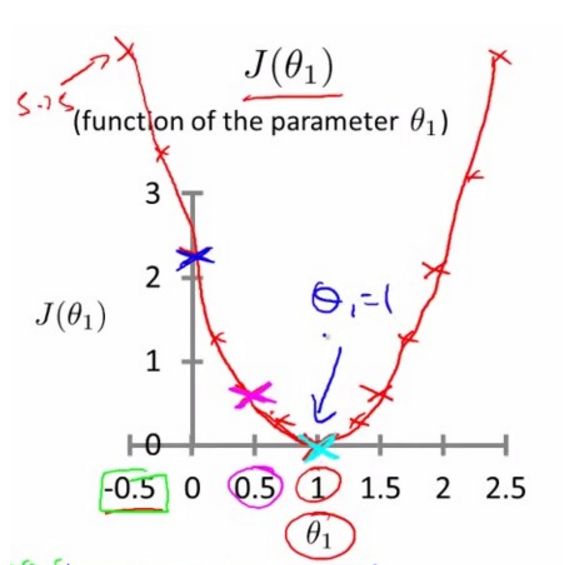
当同时考虑两个参数值 theta1和theta0时，损失函数的图像是这样的，被称为bowl-shape function，碗状的

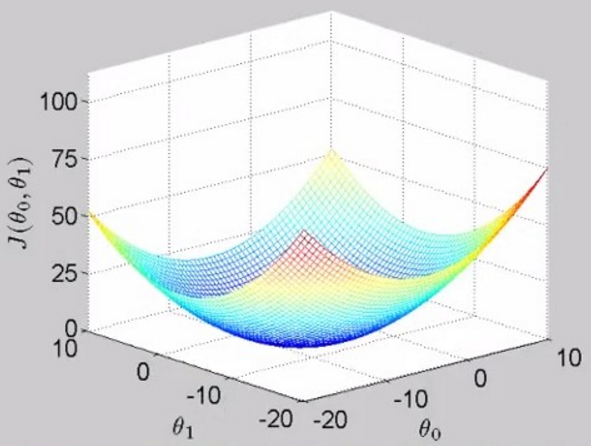
下图的右边是上面三维图像的二维展示，那一圈一圈的椭圆被称为“等高线”（类似地理上的等高线），每一个椭圆上的不同点的 J 值都是相等的，

如图中绿色椭圆上的三个点，越靠近中心的椭圆 J 值越小。

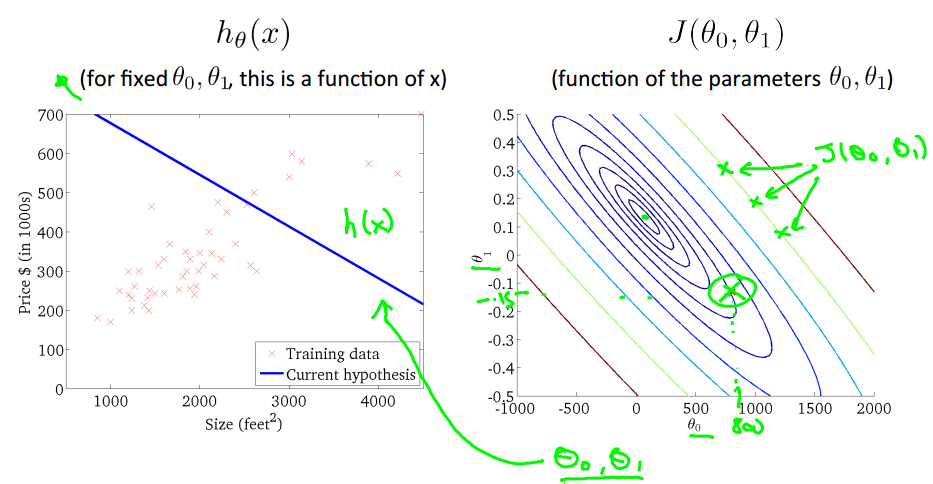
上面左图对应的是右图中用绿色圆圈标注的点（theta1=800，theta0=-1.5），对应的模型h（x）的图像，右图中每一个不同的点，

都会在左图中对应一个不同的图像，如下：

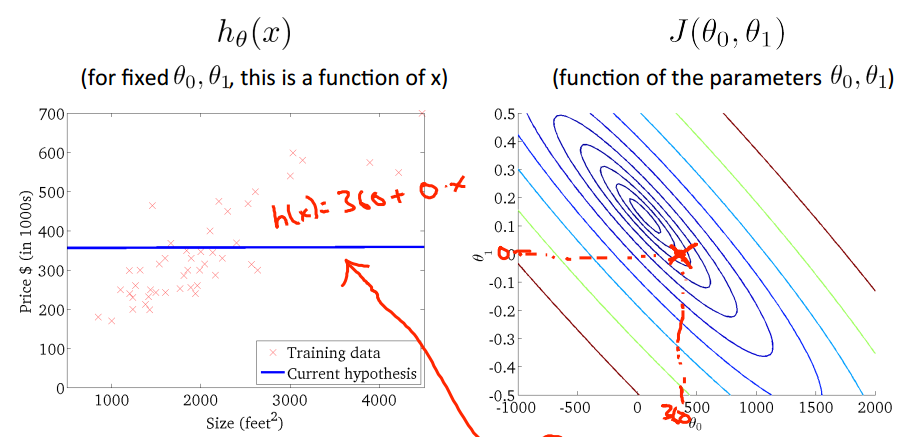
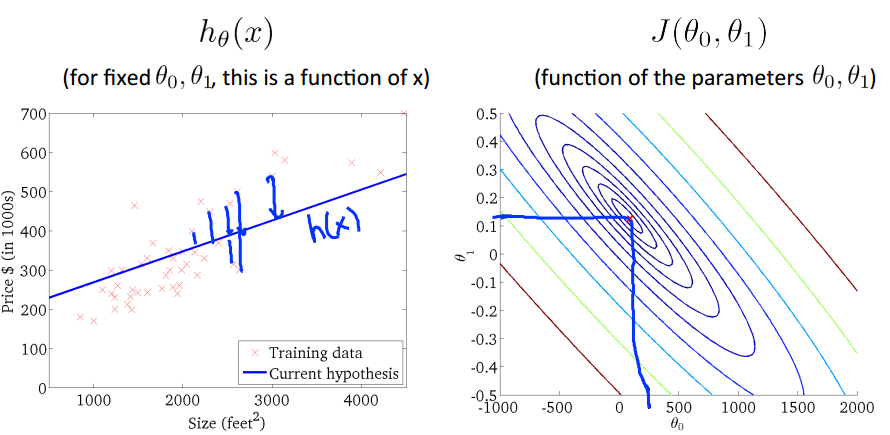
当然，我们理想的情况是类似上图的情况，我们取的（theta1，theta0）出现图中的中心theta0=450,theta1=0.12，

在这个点可以是损失函数达到最小，趋近于0.这样我们就求得了模型参数theta0和theta1，进而得到最佳的假设h（x）。

Gradient Descent（梯度下降）

我们有了假设模型h（x），和损失函数 J，现在来讨论如何求得theta1和theta0的方法，梯度下降。我们的问题描述如下：

需要不断迭代，求得使损失函数 J 达到最小的theta1和theta0.

关于梯度下降的理解：

假设你现在站在两座山包上的其中一座，你需要以最快的速度下到山的最低处。每到达一个新的地方，

都选择在该点处梯度最大的方向下山即可。如图：

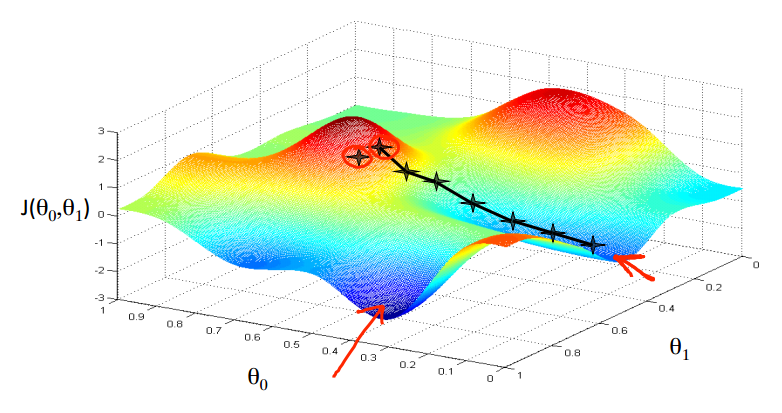
梯度下降算法表示如下：其中标出了梯度（蓝框内）和学习率（α > 0），梯度在这里通俗的说就是函数 J 的偏导数。

注意：梯度下降算法对局部最小值敏感，梯度下降可能收敛在局部最小，不能保证收敛到全局最小值。

说明：在计算机科学中，x：=x+y表示，先计算x+y的结果再赋值给变量x，类似先计算a=x+y，然后使x的值等于a。

下图为梯度为正、负的情况,theta的更新是不一样的：

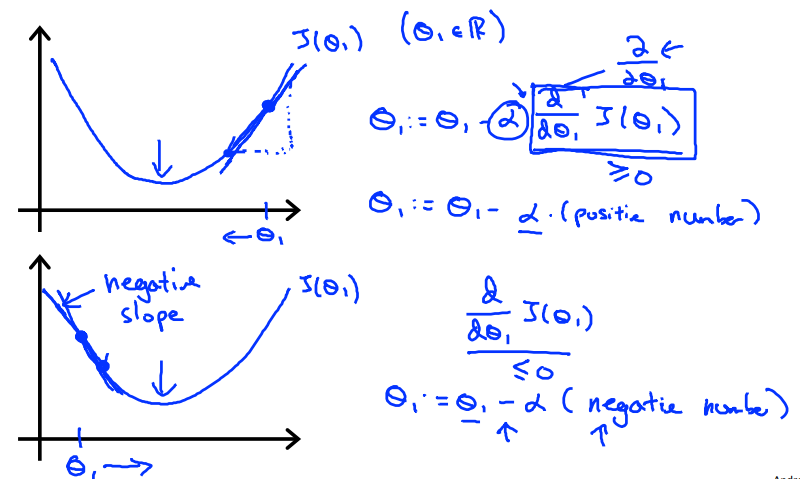
关于参数更新的问题，theta1和theta2必须同时更新，下图左边为正解，即不能使用更新过后的theta0来进一步更新theta1

（这将是后面要讲到了另一种算法）。

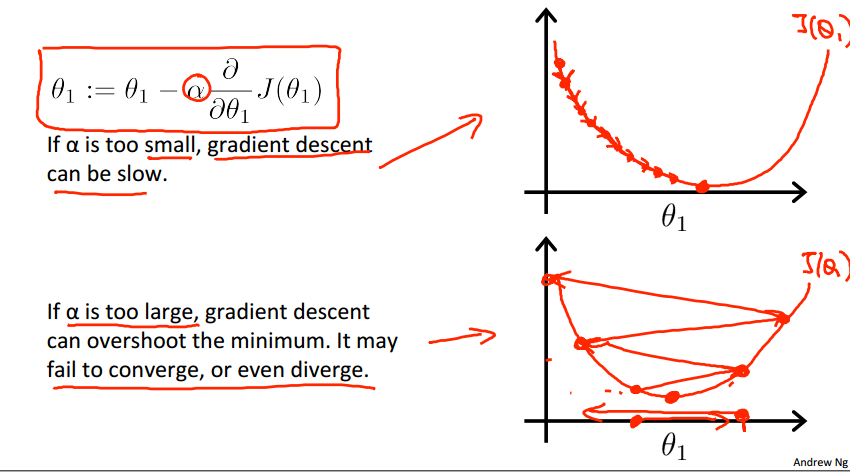
关于学习率α的问题：

当a过小的时候，迭代步长太小，梯度下降得太慢；

当a过大的时候，迭代步长过大，梯度无法收敛到最小值，而发生左右震荡的现象。

当固定a时，梯度下降法依然可以收敛到最小值（局部），

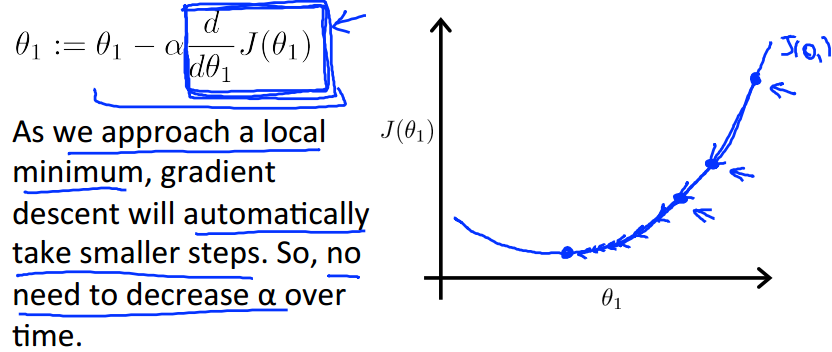
因为，当我们越靠近最小值时，我们的 梯度 越小，反应在上图就是越来越平缓，所以上面蓝色方框中的表达式会越来越小，

然后乘上a也越来越小，证明我们迭代的步长会逐步变小，即使我们使用的是固定不变的学习率a。

Gradient Descent For Linear Regression

（在线性回归中使用梯度下降）

其推导过程如下，分别对 J 求 关于theta0和theta1的偏导数：

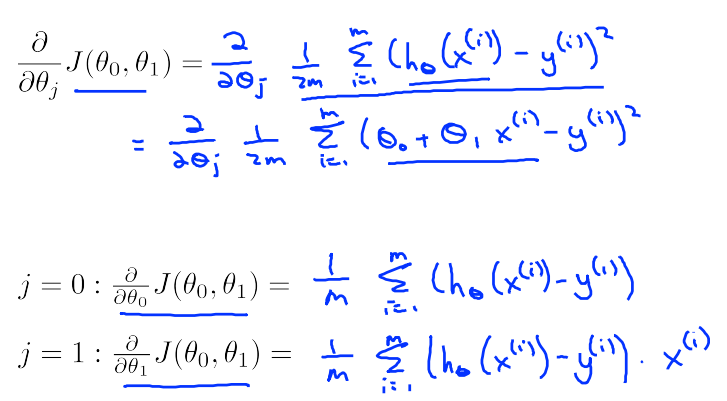
得到下面应用于线性回归的梯度下降算法：

通过对以上算法的不断迭代，我们求得了最好的假设h（x），其中红色“x”的轨迹，就是算法迭代的过程。

注：上面提到的梯度下降算法叫做“Batch” Gradient Descent，批梯度下降算法（翻译可能有所不同），其每一次迭代都需要使用整个数据集，

所以其效率不高，后面会学习到它的改进算法，随机梯度下降。

参考文献：http://blog.csdn.net/abcjennifer/article/details/7691571