hdu 5955 Guessing the Dice Roll 【AC自动机+高斯消元】

hdu 5955 Guessing the Dice Roll 【AC自动机+高斯消元】

题意：给出 n≤10 个长为 L≤10 的串，每次丢一个骰子，先出现的串赢，问获胜概率。

题解：裸的AC自动机，求匹配到终止结点的概率，用 高斯消元？一开始不知道怎么建方程组，直接举个例子吧：

Input:

1

2 2

1 1

2 1

图解：

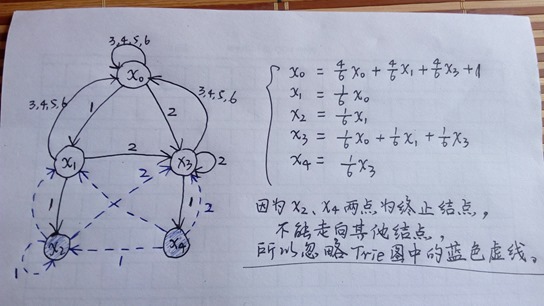
x0原本概率就是1，然后还要加上其他结点走向它的概率，，这样最后算下来是大于1的，现在还是觉得怪怪的。。。

 #include <cstdio>
 #include <algorithm>
 #include <cstring>
 #include <queue>
 #define CLR(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 const int N = ;
 const int M = ;
 int equ, var;
 double a[N][N];
 double x[N];
 void Gauss() {
     int i, j, k;
     int max_r;
     int col;
     for(col = , k = ; k < equ && col < var; ++k, ++col) {
         max_r = k;
         for(i = k+; i < equ; ++i)
             if(fabs(a[i][col]) > fabs(a[max_r][col]))
                 max_r = i;
         if(max_r != k) {
             for(j = k; j < var; ++j)
                 swap(a[k][j], a[max_r][j]);
                swap(x[k], x[max_r]);
         }
         x[k] /= a[k][col];
         for(j = col+; j < var; ++j)
             a[k][j] /= a[k][col];
         a[k][col] = ;
         for(i = ; i < equ; ++i) {
             if(i != k) {
                 x[i] -= x[k] * a[i][col];
                 for(j = col+; j < var; ++j)
                     a[i][j] -= a[k][j] * a[i][col];
                 a[i][col] = ;
             }
         }
     }
 }
 int mk[N];
 struct Trie {
     int next[N][M], fail[N], tag[N];
     int root, L;
     int newnode() {
         for(int i = ;i < M;i++)
             next[L][i] = -;
         tag[L++] = ;
         return L-;
     }
     void init() { L = ; root = newnode(); }
     void Insert(int buf[], int len, int id) {
         int u = root;
         for(int i = ; i < len; i++) {
             if(next[u][buf[i]] == -)
                 next[u][buf[i]] = newnode();
             u = next[u][buf[i]];
         }
         tag[u] = ;
         mk[id] = u;
     }
     void build() {
         queue<int> Q;
         fail[root] = root;
         for(int i = ; i < M; i++) {
             if(next[root][i] == -)
                 next[root][i] = root;
             else {
                 fail[next[root][i]] = root;
                 Q.push(next[root][i]);
             }
         }
         while( !Q.empty() ) {
             int u = Q.front();
             Q.pop();
             for(int i = ; i < M; i++) {
                 int &v = next[u][i];
                 if(v == -)
                     v = next[fail[u]][i];
                 else {
                     Q.push(v);
                     fail[v] = next[fail[u]][i];
                 }
             }
         }
     }
     void query(int n) {
         int i , j;
         CLR(a, ); CLR(x, );
         equ = var = L;
         for(i = ; i < L; ++i) a[i][i] = -1.0;
         x[] = -1.0;
         for(i = ; i < L; ++i) {
             for(j = ; j < M; ++j) {
                 if(next[i][j] != - && tag[i]==)
                     a[next[i][j]][i] += 1.0/;
             }
         }
         Gauss();
         for(i = ; i < n-; ++i)
             printf("%.6f ", x[mk[i]]);
         printf("%.6f\n", x[mk[n-]]);
     }
 };
 Trie ac;
 int main() {
     int T, n, m;
     int A[];
     scanf("%d",&T);
     while( T-- ) {
         scanf("%d%d", &n, &m);
         ac.init();
         for(int i = ; i < n; i++) {
             for(int j = ; j < m; ++j) {
                 scanf("%d", &A[j]);
                 A[j]--;    //0~5
             }
             ac.Insert(A, m, i);
         }
         ac.build();
         ac.query(n);
     }
     return ;
 }