redis的持久化方式
redis有两种持久化方式,第一种是基于快照的持久化方式,第二种是基于文件追加的持久化方式
一、基于快照的持久化
1、修改redis.conf配置文件,开启基于快照的持久化方式


2、修改持久化文件存放的位置
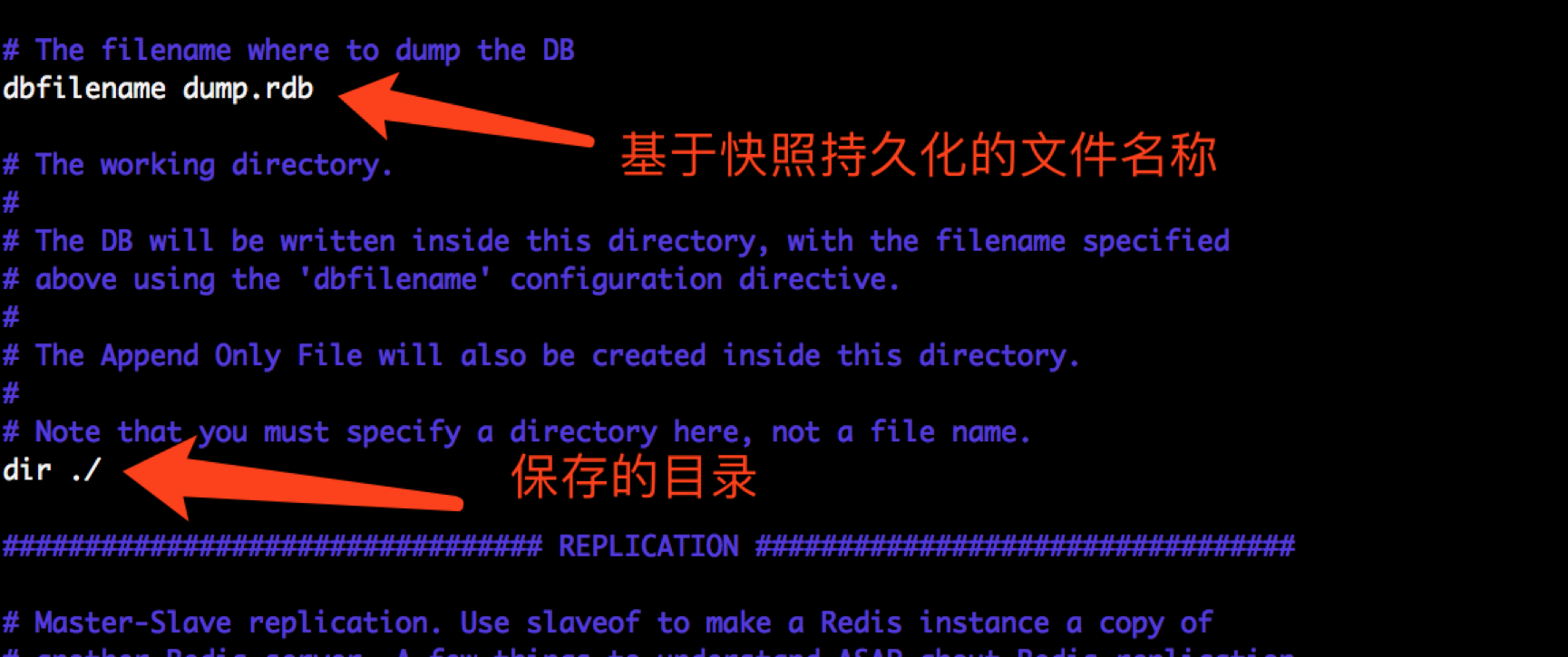
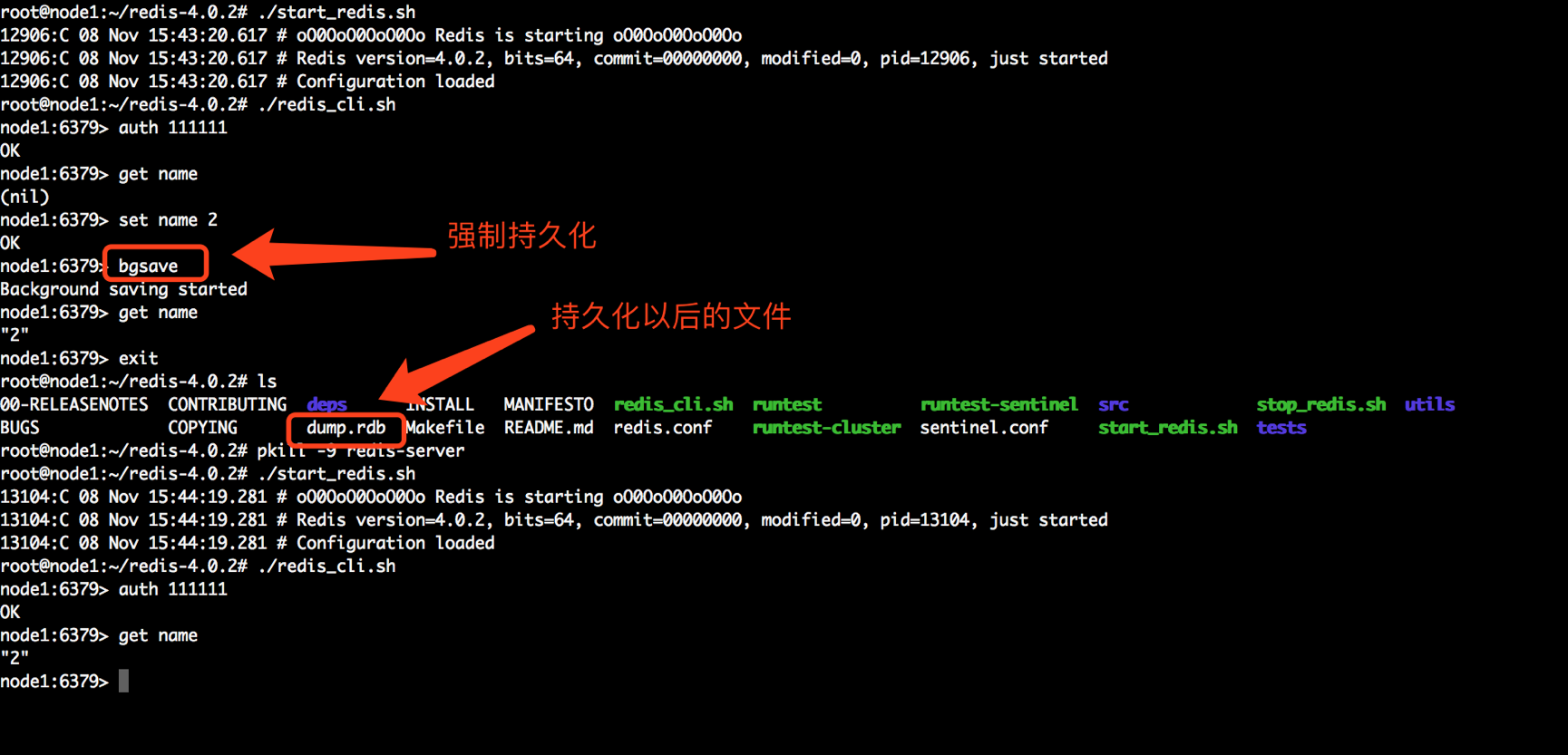
3、重启服务,测试
二、基于文件追加的持久化方式
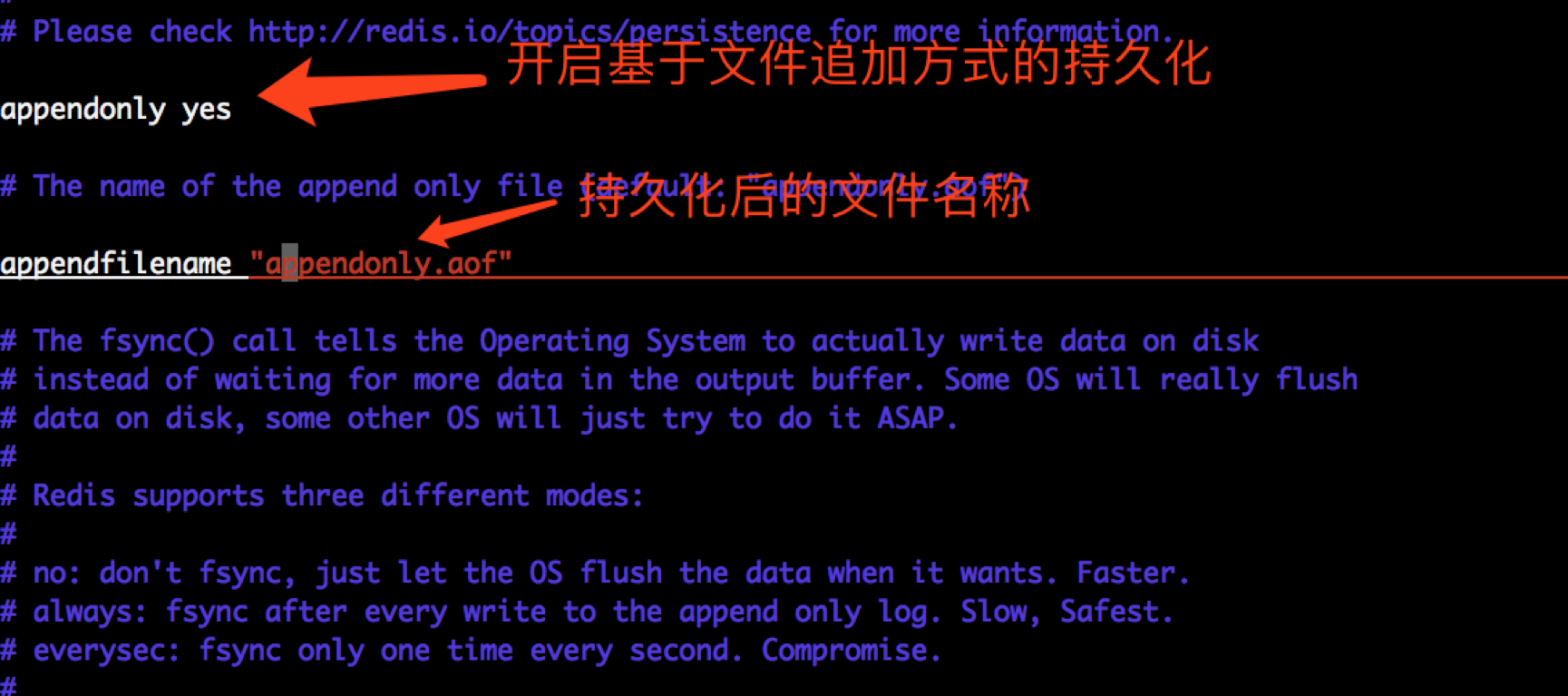
1、修改redis.conf配置文件,开启基于文件追加的持久化方式
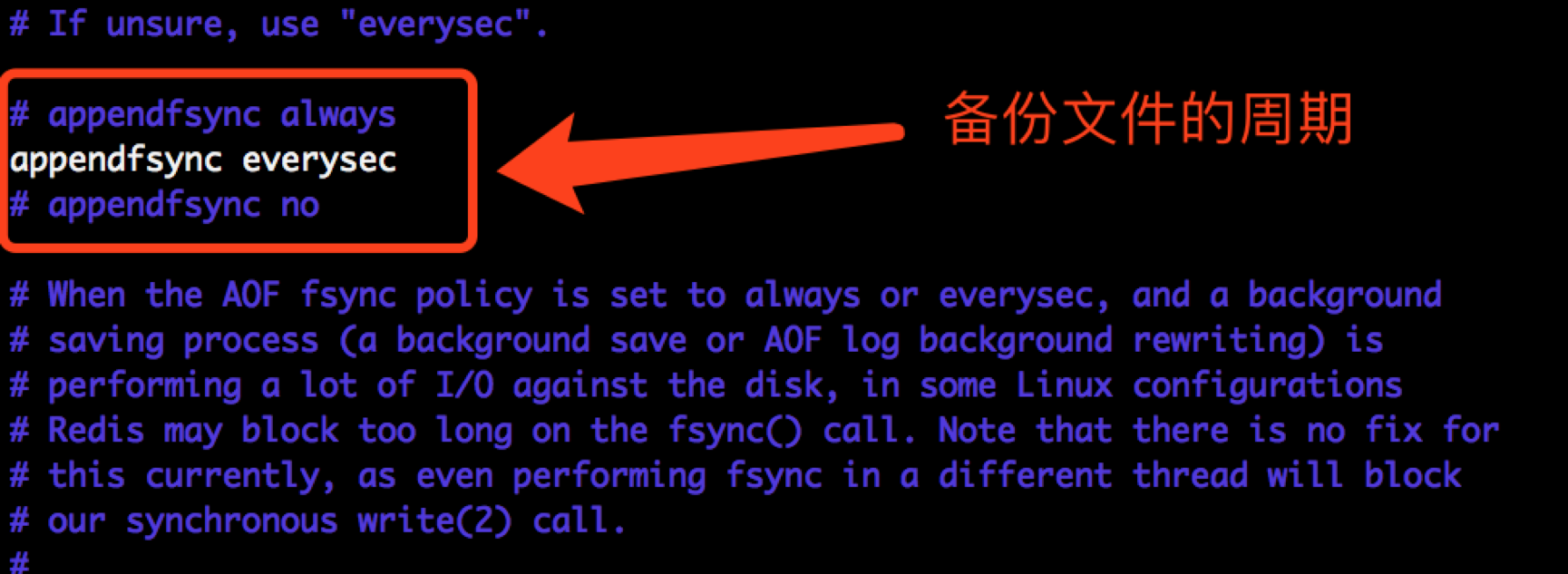
2、修改备份的周期

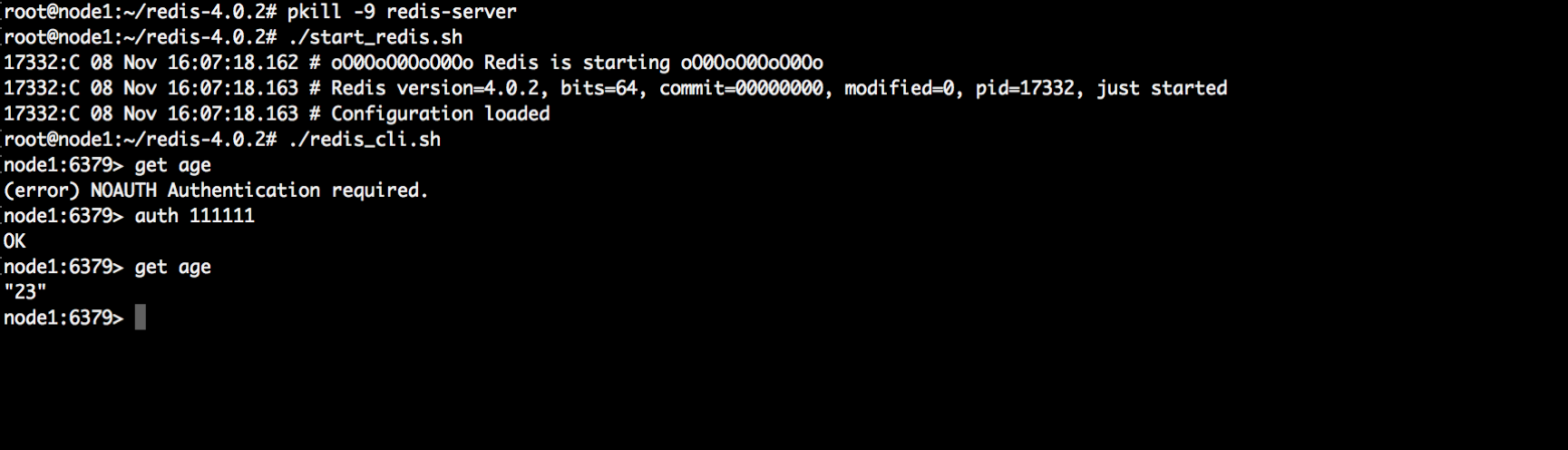
3、重启服务,测试
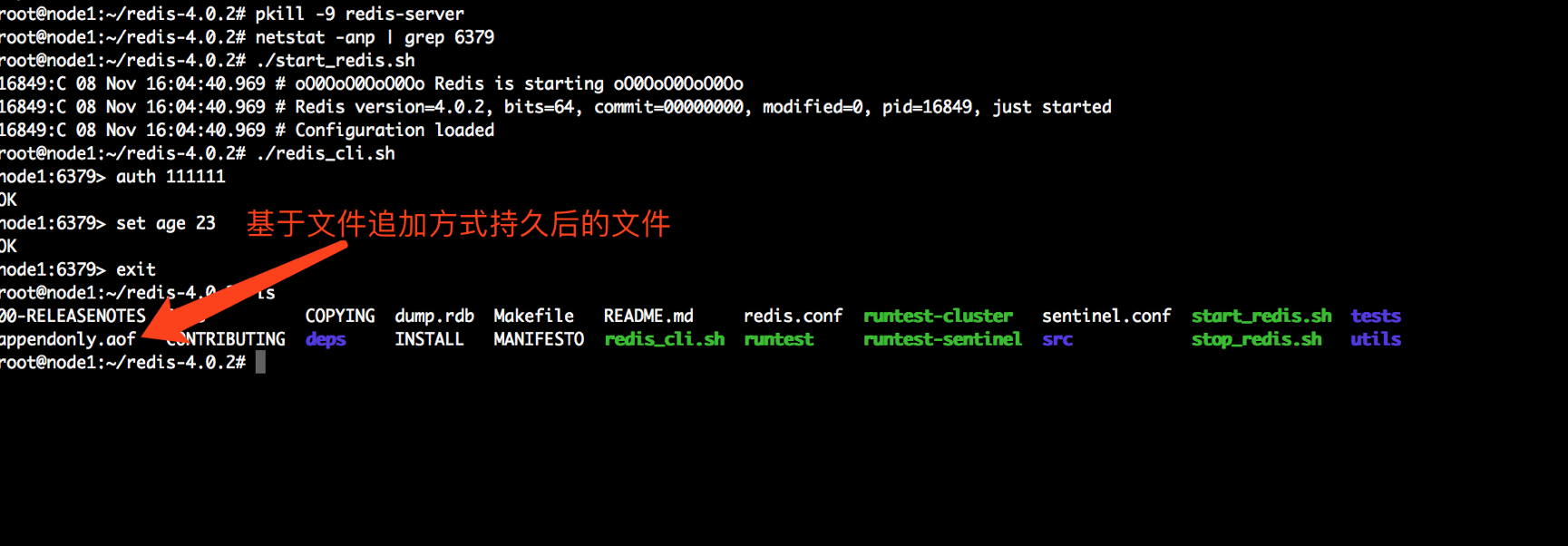
杀掉redis服务,模拟断电效果,然后重启redis服务,获取之前保存的数据,也可以获取到
redis的持久化方式的更多相关文章
- redis的持久化方式RDB和AOF的区别
1.前言 最近在项目中使用到Redis做缓存,方便多个业务进程之间共享数据.由于Redis的数据都存放在内存中,如果没有配置持久化,redis重启后数据就全丢失了,于是需要开启redis的持久化功能, ...
- 一文带你深入了解 Redis 的持久化方式及其原理
Redis 提供了两种持久化方式,一种是基于快照形式的 RDB,另一种是基于日志形式的 AOF,每种方式都有自己的优缺点,本文将介绍 Redis 这两种持久化方式,希望阅读本文后你对 Redis 的这 ...
- redis 的持久化方式
redis 持久化的两种方式 RDB:RDB 持久化机制,是对 redis 中的数据执行周期性的持久化. AOF:AOF 机制对每条写入命令作为日志,以 append-only 的模式写入一个日志文件 ...
- 分布式缓存Redis的持久化方式RDB和AOF
一.前言 Redis支持两种方式的持久化,RDB和AOF.RDB会根据指定的规则“定时”将内存中的数据存储到硬盘上,AOF会在每次执行命令后将命令本身记录下来.两种持久化方式可以单独使用其中一种,但更 ...
- Redis之持久化方式详解
背景:Redis之所以能够在技术革新发展迅速的时代超越Memcache等其他Nosql数据库,最主要的一点是Redis提供数据持久化,能够根据持久化策略将缓存数据灵活的写到磁盘上,更好地满足了当下海量 ...
- NoSql数据库Redis系列(4)——Redis数据持久化(AOF)
上一篇文章我们介绍了Redis的RDB持久化,RDB 持久化存在一个缺点是一定时间内做一次备份,如果redis意外down掉的话,就会丢失最后一次快照后的所有修改(数据有丢失).对于数据完整性要求很严 ...
- 详细分析Redis的持久化操作——RDB与AOF
一.前言 由于疫情的原因,学校还没有开学,这也就让我有了很多的时间.趁着时间比较多,我终于可以开始学习那些之前一直想学的技术了.最近这几天开始学习Redis,买了本<Redis实战>, ...
- Redis两种持久化方式(RDB&AOF)
爬虫和转载请注明原文地址;博客园蜗牛:http://www.cnblogs.com/tdws/p/5754706.html Redis所需内存 超过可用内存怎么办 Redis修改数据多线程并发—Red ...
- Redis的持久化的两种方式drbd以及aof日志方式
redis的持久化配置: 主要包括两种方式:1.快照 2 日志 来看一下redis的rdb的配置选项和它的工作原理: save 900 1 // 表示的是900s内,有1条写入,则产生快照 save ...
随机推荐
- 【转】ListBox Dock Fill 总是有空隙的问题
源地址:https://www.cnblogs.com/norsd/p/6359291.html ListBox Dock设置了Fill, Right等 设计界面如己所愿,但是实际运行时,底部总是有不 ...
- Elasticsearch NEST使用指南:映射和分析
NEST提供了多种映射方法,这里介绍下通过Attribute自定义映射. 一.简单实现 1.定义业务需要的POCO,并指定需要的Attribute [ElasticsearchType(Name = ...
- 跟刘欣学习造spring
1: 读取配置文件并获取对象实例
- PHP查询数据库,对象结果集转化为数组
$row = $this->db->get();//得出对象结果集 $result = array(); if($row) { //转化为数组 while($value = $row-&g ...
- 最小生成树(Prim算法+Kruskal算法)
什么是最小生成树(MST)? 给定一个带权的无向连通图,选取一棵生成树(原图的极小连通子图),使生成树上所有边上权的总和为最小,称为该图的最小生成树. 求解最小生成树的算法一般有这两种:Prim算法和 ...
- sudo: /usr/bin/sudo must be owned by uid 0 and have the setuid bit set
使用root 登录,然后执行: chown root:root /usr/bin/sudo chmod 4755 /usr/bin/sudo reboot
- 基础篇:4.2)规范化:3d软件工程图纸用模板
本章目的:分享一些国标标准模板,方便作图时使用 这篇博文的内容作者会定时的更新 1.工程图模板 drawing template 定义 三维机械设计软件中的一种文件类型.通过标准化定制和使用该文件,可 ...
- linux普通用户免秘钥登录(xshell工具环境)
一.xshell生成密钥 1)工具->新建用户密钥生成向导 2)选择密钥类型.密钥长度(默认即可) 3)生成密钥(生成公钥和私钥) 4)为密钥加密,增加密码(可选),建议加上 5)将公钥保存为文 ...
- Linux 远程登录ssh服务器
1.安装ssh服务器 sudo apt-get install openssh-server 2.在另一端输入ssh IP及密码(或ssh 用户名@IP)就可以远程登录到IP所在计算机
- lua table、ipairs/pairs基础知识
1.什么是table? table是Lua最复杂最强大的数据结构,Lua本身并不是面向对象语言,但是对面向对象中毒比较深的程序员,可以借助table”完美”地模拟面向对象编程.最简单地,我们可以把ta ...
